Why Are Great Circles the Shortest Flight Path?
Why do you fly over Greenland in an airplane flight?
Or why is it that when you see flight paths on a map they always take a curved route between 2 cities?
It’s because planes travel along the shortest route in a 3-dimensional space.
This route is called a geodesic or great circle route. They are common in navigation, sailing, and aviation.
But geodesics can be confusing when you’re looking at a 2-dimensional map as they follow quite the odd flight path. Let’s dig into this concept a bit deeper.
Great Circle Routes Explained
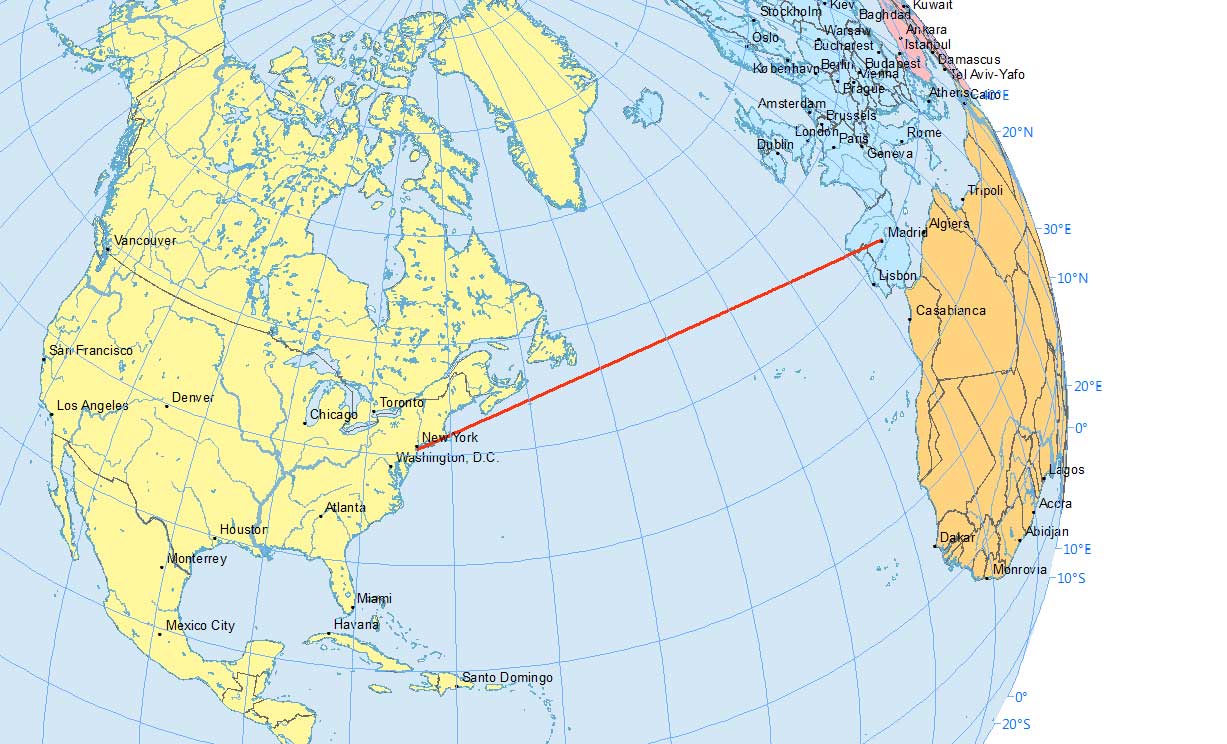
In a flight path from New York to Madrid, if I asked you which line is shorter, you’d say the straight one, right?
However, a straight line in a 2-dimensional map is not the same as a straight line on a 3-dimensional globe.
This is why flight paths travel along an arc between an origin and a destination.
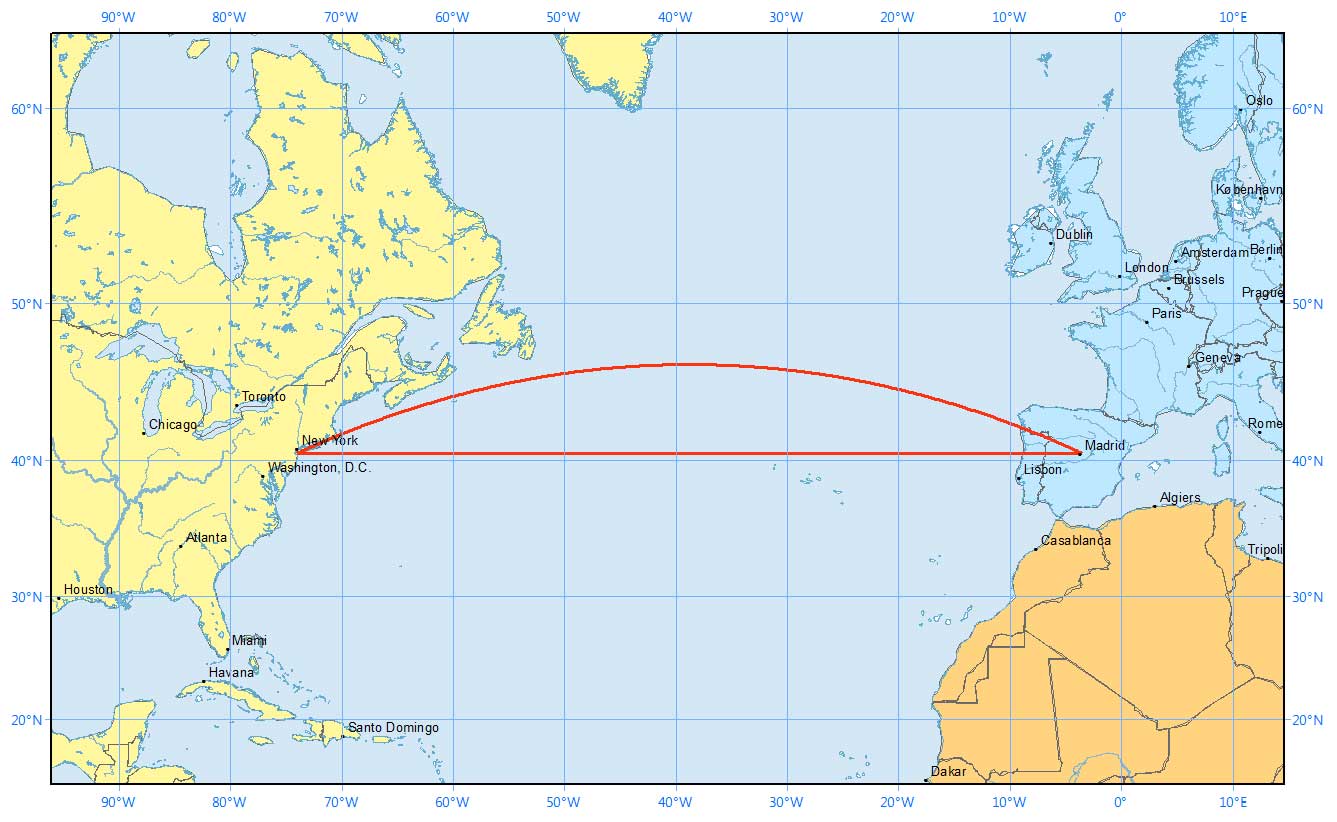
Now here’s what the same flight paths look like on a sphere. Remember that the straight line in the Mercator map above followed the 40° latitude line.

This paints quite a different story, doesn’t it? It’s deceiving to the human eye.
The takeaway is this:
A route that looks longer on the map is because of the distortion created by map projections like the Mercator Projection. In navigation, pilots often use great circles (geodesic) as the shortest distance flight.
Great circles vs small circles
Now that you have a visual understanding of great circles. Here’s a definition of what a great circle is:
- A great circle is a circle on the globe such that the plane passing through the sphere’s center is equal to the circumference of the Earth.
- Alternatively, a great circle is where the radius is equal to that of the globe representing the shortest distance between two points on the surface of the earth.
In basic terms, imagine you’re cutting into an orange. You can cut them at any angle – north-south, east-west, diagonally. As long as you cut two identical portions, then the circle where the cut was made is a great circle.
For example, the equator is a great circle because it’s the maximum possible circle:
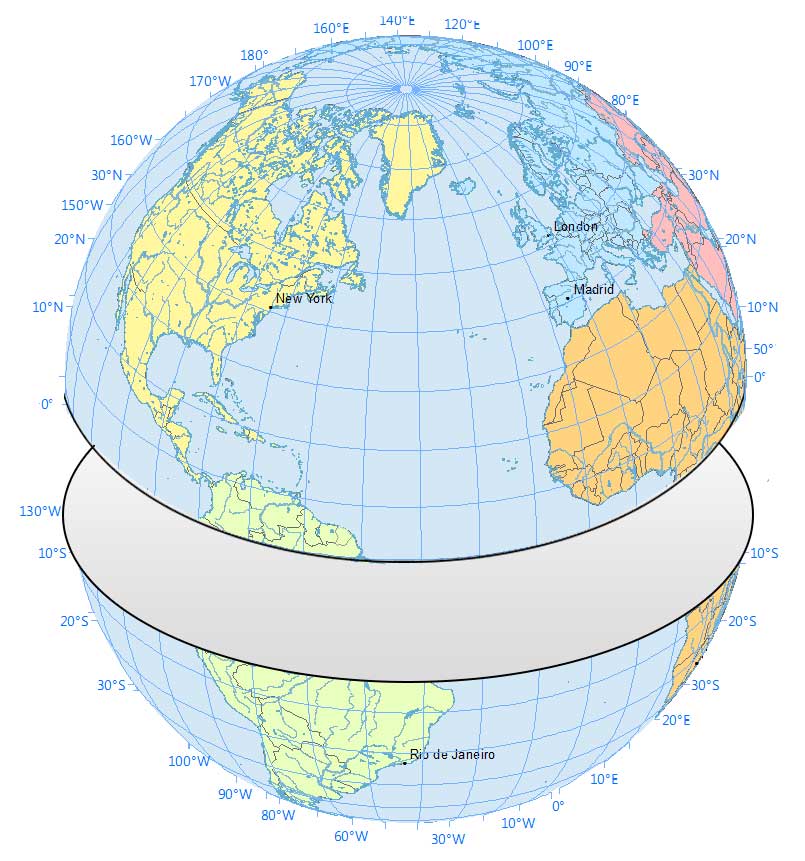
You could also cut it at the north and south poles. This longitudinal line also cuts two equal portions. Any meridian line is a great circle as well.
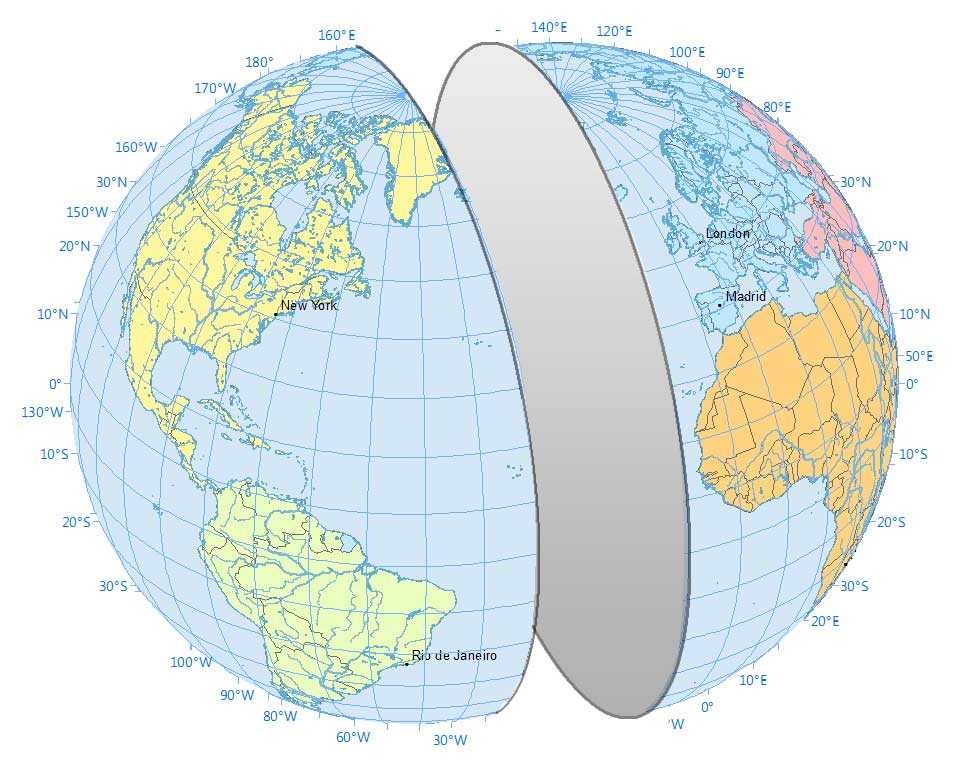
From New York to Madrid, here’s how the plane creates two equal segments.
A great circle generates two arcs with the shorter one being the shortest path. Here is the shortest path and how the plane is angled to create the shortest path.
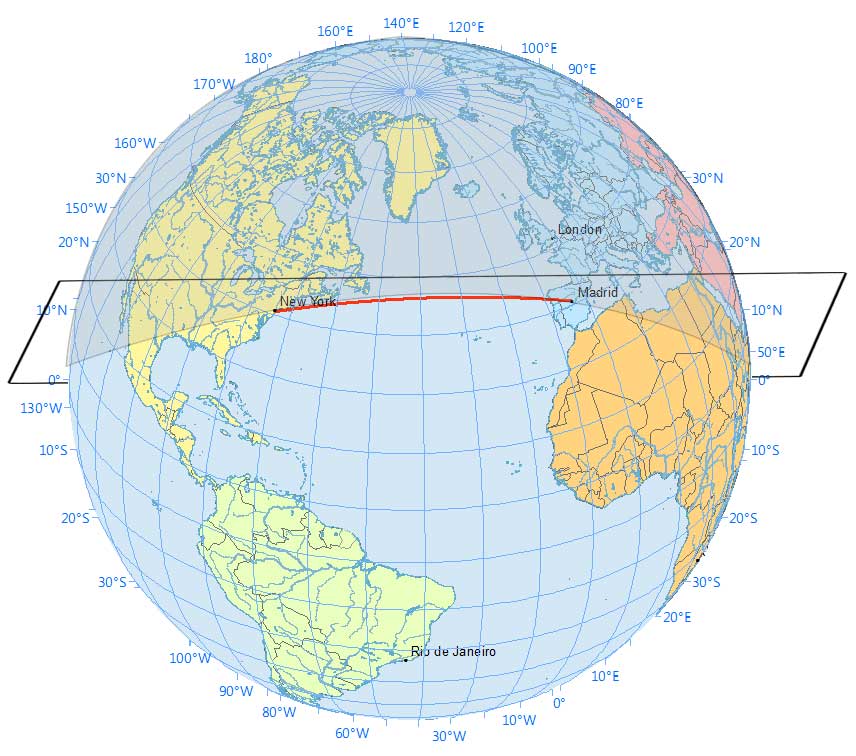
How about when you follow along the 40° latitude line? Anywhere that it doesn’t cut two equal pieces is a small circle.
While a rhumb line track is at a constant azimuth, a geodesic line changes direction all the time.

This fundamental difference in navigation concepts can have a significant impact on long-distance sea voyages.
How Geodesics Work
Planes travel along the shortest route in 3-dimensional space. This route is called a geodesic or great circle.
While map projections distort these routes confusing passengers, the great circle path is the shortest path between two far locations.
This is why pilots fly polar routes saving time and distance. And this is why pilots often fly over Greenland.
Have any questions? Please let us know in the comments section below.





can you say how to prove for shortest path for n dimensional sphere?
Please, I want to use your draws in a aerodynamic book for engineering students (in spanish language).
Please, can you report me if I can use it?. In case of yes, wich will be the conditions?
kind regards !!!
Hi Victor. In this case, you can use these images. We are the creators of these graphics. Check out our guide how to cite – https://gisgeography.com/how-to-cite/
Hello! Thank you very much! My reply is a little late, but someone found my notebook before I lost it. I had lost your address; I only just found it by chance, and that’s why I’m replying now. Forgive the lack of courtesy, but I thought the address was only in the notebook.
Way to conflate 2 different idioms:
“This paints quite a different story, doesn’t it?”
I think one paints a different picture or tells a different story. How does one paint a story, or tell a picture?
Otherwise, a great article.
Buy a globe and figure it out.
I’m trying to figure out what flight path an LTA aircraft (Larger than Goodyear Blimp) would take from England to Idaho. It’s part of a novel I’m writing. Any suggestions?
You’re definitely on the right path and to use a great circle.
I am a layman. Please describe the route from Mumbai to New York and San Fransico to Tokyo through a diagram to show why airlines prefer polar routes?
A great circle connecting two points is the shortest distance but it requires frequent heading changes throughout the journey. A straight line (rhumb line) drawn on a Mercator projection map produces the constant compass bearing to follow for the same journey; which is easy to draw and much easier to follow. Over a short distance the difference between a great circle and a rhumb line route is negligible so the simple rhumb line route is used. However, over a very long journey the difference in distance will be quite significant so a great circle route is preferred.
In navigation latitude is the angle above (north) or below (south) of the equator. Longitude is the angle east or west of the prime meridian (ie the Greenwich Meridian). Both of these angular measurements are derived from the centre of the global earth mass. 0 degrees latitude, 0 degrees longitude is the intersection of the prime meridian and the equator (just south of Ghana West Africa).
When you try to draw a flat map to depict the surface of a globe there is a huge problem; imagine taking the peel off of an orange and trying to lay it out flat.
On the surface of global earth the horizontal distance measured between two meridians along the equator (0 degrees latitude) will be greater than the distance between the same two meridians measured along any other latitude because the circumference of each latitude gets smaller toward the poles so the meridians are closer together near the poles. However, the distance measured between two latitudes on the same longitude is the same distance on other longitudes because they will lie on a great circle.
For marine navigation the map solution generally accepted is the Mercator projection because of its unique property of representing any course of constant bearing as a straight segment that can easily be drawn on a flat map. Such a course, known as a rhumb line, is preferred in marine navigation because it is easier for a ship to sail in a constant compass direction to reach its destination even though it will be a bit further than a great circle route. For short distances the difference between the rhumb line and great circle route is negligible. For aviation the distance is more critical since it directly affects time, fuel and load. A simple solution is, where possible, create a sequence of short rhumb lines along the corresponding great circle route. In the modern era all of these positioning problems have been overcome by GPS satellite navigation.
These days we all take degrees latitude and degrees longitude for granted because they have been successfully used for over 2,000 years. Around that time there were early attempts to measure the circumference of the global earth. Early mariners setting off on long voyages either came ‘back’ or never returned; which for millenniums gave rise to the flat earth notion. The first circumnavigation of the earth was accomplished by the Magellan fleet sailing westward 500 years ago. I’ve personally used latitude and longitude to circumnavigate the earth 5 times.
I’ll finish with a reminder that latitude and longitude are both angular measurements derived from the centre of the global earth mass. If the earth were flat then for positioning on it there would be only one angle from the centre and a linear distance measurement from it… an idea that has never ever been tried and proven.
Taking all of the info from this page into consideration, how could it be used to strengthen flat earth theory? I was directed here because I wanted to learn what constitutes a “great circle” and I now understand. I seriously want to know how anyone could reach that conclusion.
High-altitude flying brings another problem to the fore. It is called “coffin corner” where if you fly slower you will stall, and if you fly faster you will also stall.
It actually makes sense if you go back to the comparison of cutting an orange. Again understanding how to navigate along a 3-dimensional globe while looking at a 2-dimensional picture is why it seems so confusing. And No Cari it doesn’t support the flat earth theory. Not even its own theory supports it. lol. The entire point of this is because of it’s a globe. If it were flat none of this would be necessary. Not to mention the Japanese would still be en route to Pearl Harbor if it were a flat earth. That’s an exaggeration but still, it would have been quite a long flight. One that those little planes would never have been capable of making. In fact, if the earth were flat many lives at Pearl Harbour as well as at both Hiroshima and Nagasaki would have been spared. It’s a shame that the earth is in fact round.
You have supported the theory of a flat earth. Thanks.
My wife just left Dallas for Tokyo. I looked on the flight plan and it goes up through Montana and Canada and over the edge of Alaska. I don’t see how this could be the shortest route to Tokyo from Dallas. It seems more like they are trying to avoid flying directly over the vastness of the Pacific Ocean in case there is a mechanical problem.
Having read all the above I’ve decided to go by boat.
Odd! I was told that because of centrifugal force, the Earth was compressed at the poles, thus making it wider at the equator.
The great arc is a navigational compensation!
Meanwhile, the Egyptians, who started all this, still could not figure out the height of the pyramids even though they had Pythagoras. Not to mention that even today there is no certain way to measure the partial volume of a cylinder.
The Earth is flat and south polar centered. That’s it.
What about the direction of the route? Nobody can convince me that Madrid lies to the north of Newyork as they are saying now.
Maybe thats how they conclude it but its wrong, even if it works. the real reason is because of difference of rotational velocity of a shorter vs longer circumference. if you draw two lines from the center of a circle, each come out of the destinations. then draw two lines, one at altitude and the other at ground level. clearly the one at altitude is longer. it doesn’t matter if these lines are curved or not. what matters is the velocity the earth rotates at. the length of a circumference increases by 2 pi r. this means that at greater radius per starting location, the rotational velocity of a shorter radius vs a larger are varied. at a great altitude, though you are traveling at a perceived pace relative to the motor function, but you are multiplying that velocity by the increase in circumference relative to the ground’s. or vice versa, you can say the ground it traveling quicker as well since two point in the circumference have less distance to travel compared to the greater altitude. but what this really does is multiply the distance you travel at altitude relative to the ground. so one minute of flight at ground level vs one minute of flight at altitude results in greater distance. but its only if you fly against earth’s rotation. the earth is rotating at a constant speed, but the circumference between the greater height points travels at length over time just as the shorter one. but the shorter circumference then has less length to travel in that time, so its technically traveling slower. so as you increase height from the center of a circle, the increase in circumference, with earth’s rotation increase your velocity. if earth wasn’t rotating, then height wouldn’t matter and straight line would. 3 dimensions or 2… sure, you could look at it that way, but its over complicated…
Because the time it takes to fly to the higher altitude is not commensurate to the time lost by not climbing.
Let P = pressure, d = density, R = gas constant, T = temperature, h = height, g = gravitational acceleration.
By Ideal Gas Law
PV = nRT -> d = n/V = P/RT
By the law of hydrostatic pressure
dP/dh = -d*g = P*g/RT
We know have a first-order separable differential equation. Solving this, we get:
Integral dP/P = Integral -g/RT dh
log(P) – log(P0) = -g*h/RT -> P = P0*exp(-g*h/RT)
d = P/RT = P0/RT*exp(-g*h/RT)
Therefore, as you go higher, the weight of the air column decreases reducing atmospheric pressure and density. However, the air also gets colder slightly increasing density. In the Stratosphere, temperatures increase with altitude instead of decrease. However, this layer of the atmosphere is above the troposphere where we live, so it has to be less dense. Thus, the weight of the hydrostatic pressure of the air column has a larger effect on atmospheric pressure and air density at least less than 10 km above sea level.
In the real world of long distance air navigation, great circle routes are *not* the shortest *flight* path, but they do make a good start on figuring out what will be the shortest flight path. The article fails to understand that aeroplanes travel in the air, which is moving, rather than fixed in relation to the earth. The origin and destination are fixed to the earth, if the sea and the air were likewise fixed, a great circle would yield the shortest path. A longer path with regard to the earth can yield flight path savings in the order of 30% to 50%, the classic example being North Atlantic flights in the forties, where savings of this order resulted from using Bellamy drift derived constant heading paths instead of great circle routing.
Aircraft need to travel the shortest route in the air, not in three dimensional space. Sometimes that will be the same thing, but not very often. For an air routing, you could use the barometric pressure at origin and destination plus the latitudes. Using these, you can calculate the drift for the entire flight due to pressure differences and Coriolis effect, the net geostophic winds. However, there may be jetstreams at less optimum altitudes that could provide considerable net improvement, even if more fuel is used per air mile (meaning movement through the body of air, not the 3D relationship with the earth), but lets not go there. Having derived a constant heading, it is flown, and neglecting political geography, with no concern for the position with respect to the position on earth below, other than the destination and not bumping into things.
To help with the lay understanding, imagine a rectangular table top, with a dot at each end. Over the top you have a much larger piece of perspex. You have a toy car which can travel at a speed equal to the distance between the dots over one hour. Over the course of an hour, the perspex moves half that distance to the left of the direct track, then half that distance to the right. If we attempt to stay on the “shortest” path from A to B, at the end of an hour, we will still be at A. If we calculate the net drift between A and B, which in this example means following a constant heading equal to the direct heading at the start of the journey, our path will be much longer than the direct path, a loop heading out to the left. However, after an hour, we will be at B. If we change the total distance moved by the perspex to half A-B, purely left and right, it will still take us one hour on the constant heading, but if we follow the direct path on the table top, we will get there, having taken considerably more than an hour to do so.
On shorter journeys in the real world, there are few wind reversals – there is also little difference between a rhumb line course and a great circle, so you may as well fly a rhumb line. Longer journeys are where this counts, and also where the great circle should be of use, but often is not, due to winds aloft.
The correct term is “Density altitude” which is a calculation of pressure altitude corrected for nonstandard temperature. As temperature and altitude increase, air density decreases. All aircraft have a flight “ceiling”, an altitude above which it cannot fly. As an airplane ascends, a point is eventually reached where there just isn’t enough air mass to generate enough lift to overcome the airplane’s weight. This is why (depending on the airplane) you might not be able to take-off from a high altitude airport on a particularly hot day. I have experienced this (pilot) myself several times.
If you depart from the North Pole with a plane along a meridian, directly from the rotation point (rotation axis) where speed is 0, to a destination at the equator where the rotation speed is around 1660 km / h , would the plane still reach its destination?
From North Pole direct to Brazil(circular arc over meridian 60 W).
Thinner air does not give better engine performance. The reason flying high is more economical compared to flying at low altitude is because the TAS is higher due to density. Thus the amount of fuel burned per nm travel is lower.
You have such great figures. May I use one of them in a presentation to illustrate great circle routes?
Yes, you can. But please give credit by referencing to gisgeography.com
Chris, you are wrong. For air, D=PM/(RT), where D=mass density, P=pressure, M=molecular weight average, R=ideal gas constant, & T=absolute temperature. This is why you need to fill your tires with air in the winter. The temperature drop compresses the air, which means you have to add air to fill in the same amount of relative space.
There are many other atmospheric factors in play such as humidity, wind speed, and wind direction to consider as well.
…and yes, thinner colder air is better for fuel efficiency, but bad for lift. The higher you go, the harder it is to maintain altitude, so like everything else, there is a trade-off. Airplanes are designed to take advatange of the thickness of the air at a certain altitude. That altitude is not fixed relative to the ground, but depends on the weather. So on a hot day, they can fly higher. On a cold day, they.have to fly lower. But there is always an optimum “temperature altitude” for any given plane on any given day. You can’t just keep going up forever. You need pressure under the wings, or you’re flying a brick.
Airplanes need air pressure to fly, it doesn’t matter how dense the air is if there’s no pressure, and pressure and altitude have a consistent relationship. Does that make sense?
Actually, you’re all right, but you’ve each only got two-thirds of the puzzle. There is no direct relationship between temperature and density. There IS a relationship between PRESSURE and temperature and density.
In aviation, there is a concept called “termperature altitude.” So the actual relationship is between all three of them, but the focus is only on the two. The higher you go, the colder and thinner the air gets because the pressure is dropping. For every 1000 feet you go up, there is an expected drop in temperature and pressure, and this remains constant. So flying through colder air is like flying higher. The colder air makes the pressure go down while the density remains the same. The airplane acts as if the air is less dense. Got it?
I too, like Mr. Bir, noticed that there was something wrong with the explanation regarding the density of air. Yes, as air gets colder it gets denser, that’s why to start a cold gasoline engine you have to activate the ‘choke’ which in turn will supply the fuel-air mixture with an extra amount of fuel in order to compensate the leanness that otherwise would not start a combustion.
J Bir, unlike liquids the viscosity of gases inceases with increasing temperature. This can be explained using the kinetic theory of gases.
Mr Bir has it right on, as soon as I read it, I questioned it. But we appreciate your explanation of the great circle route. Good article.
Let me correct you. As the air gets colder, it gets denser, not thinner. However, as you increase in altitude, the air gets thinner and colder. Pilots will always want to fly higher as the low density of the air reduces drag and thus increases the efficiency of the fuel.
Every airline in the world has a business route. This route determines where the aircraft can and cannot fly. For example certain routes over the Atlantic are more costly to make but much faster, the final determination is down to the pilot, in regards to how much fuel he has on board, how delayed the aircraft is, in respect to flying faster than he normally would. This is a very significant thing when determining which transatlantic route to take, because there are at least a dozen of which only 3 of those routes are the fastest and most economical, the rest vary with flight cost.
In respect to flying over Greenland, there was a very valid reason to do so especially during the winter and early spring months. As the air gets colder, it gets thinner, and the air thins it gets more and more difficult for an aircraft to stay in the sky. This meant under aviation rules, those aircraft with only 2 Jet Engines had to make the shortest distance between land masses, incase an engine stopped working. This way the pilot could make an emergency landing. Aircraft such as the 747 had no such problems, and could easily fly the quickest transatlantic routes. However over the decades Jet Engines have become increasingly reliable, so much so, that they too can now fly over the Arctic to whatever destination.
There are very few airlines who actually use Arctic routes, because these routes are extremely expensive to use.
An example of a flight from Helsinki (EHFK; HEL) to Barcelona (LEBL, BCN) does not use a Great Circle nor a Small circle, it uses a direct path from point A to B.
Small circles are not always used for short distances, infact they are seldom used in Europe. Instead most short distances are literally from A->B.
Why are small circles used in short distance trips and not the latter?