How GPS Receivers Work – Trilateration vs Triangulation
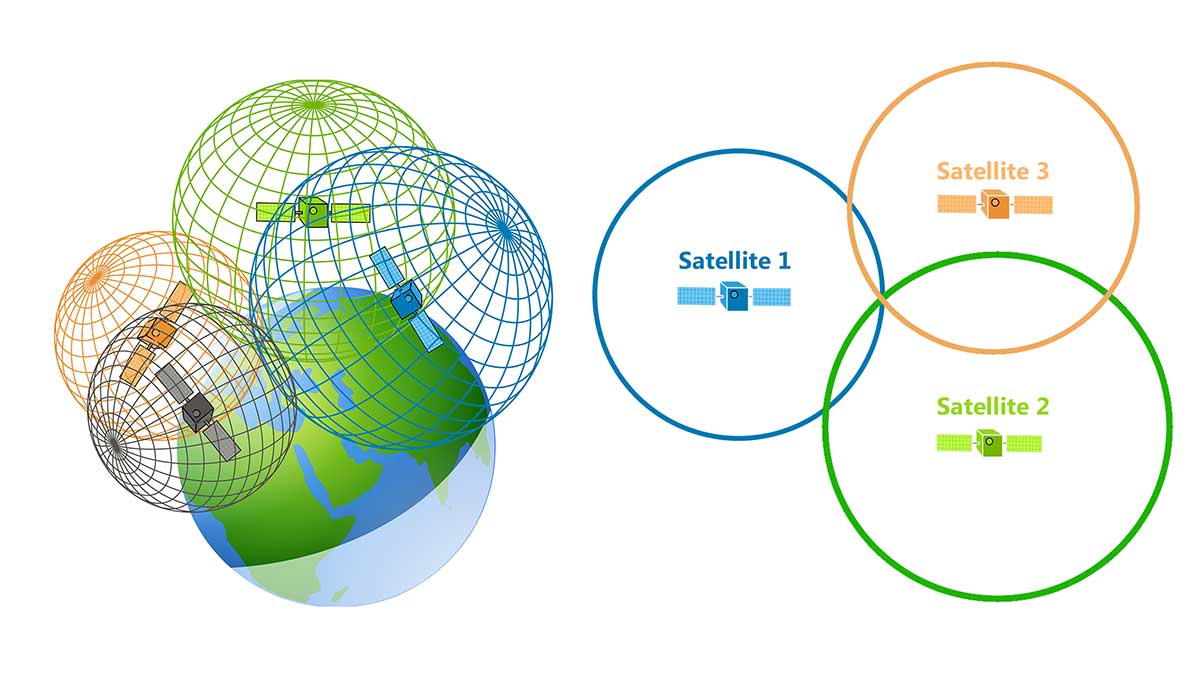
GPS Receivers Use Trilateration
Have you ever wondered how your GPS receiver works? They use a technique called trilateration.
Despite how GPS receivers are often confused with triangulation (which measures angles), they really don’t use angles at all.
Trilateration involves measuring distances.
Let’s take a look into this with a bit more detail.
Trilateration Measures Distance, Not Angles
How does the GPS system pinpoint your location using trilateration?
Using a simple two-dimensional example, let’s imagine we have three GPS satellites each with a known position in space.
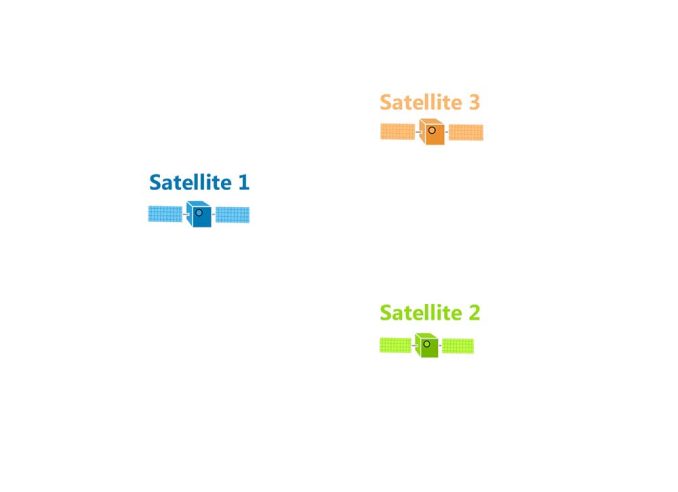
Really, all that satellites do is broadcast a signal for your GPS receiver to pick up with a specific time and distance.
For example, the first satellite broadcasts a signal that eventually hits your GPS receiver. We don’t know the angle, but we do know the distance. That’s why this distance forms a circle equal in all directions.
This means that your GPS position could be anywhere on this circle at this specific radius.
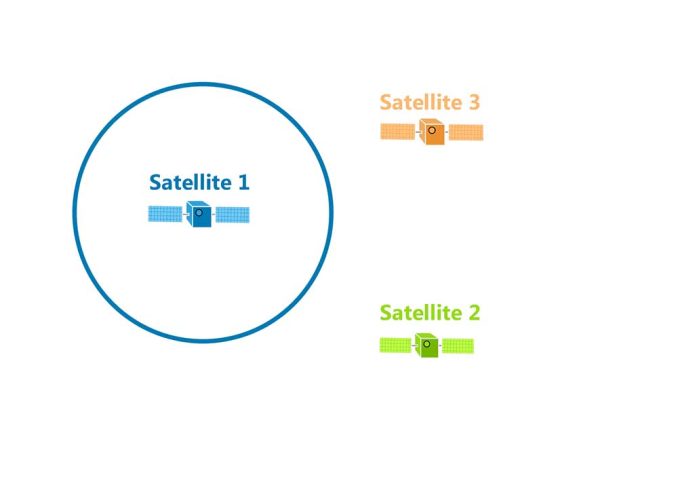
What happens when your GPS receives a second signal?
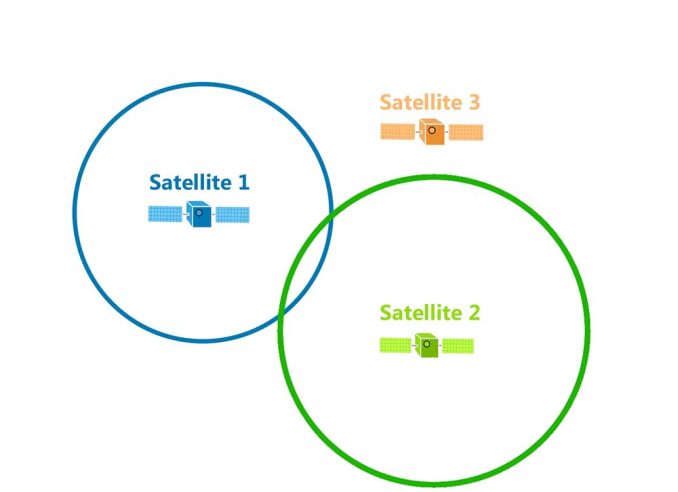
Again, this distance is equally broadcasted in all directions until it hits your GPS receiver. This means that the distance could be anywhere on that circle.
But this time, we have two known distances from two satellites. With two signals, the precise position could be any of the two points where the circles intersect.
Because we have a third satellite, it reveals your true location where all three circles intersect.
Using three distances, trilateration can pinpoint a precise location. Each satellite is at the center of a sphere and where they all intersect is the position of the GPS receiver.
As the position of the GPS receiver moves, the radius of each circle (distance) will also change.
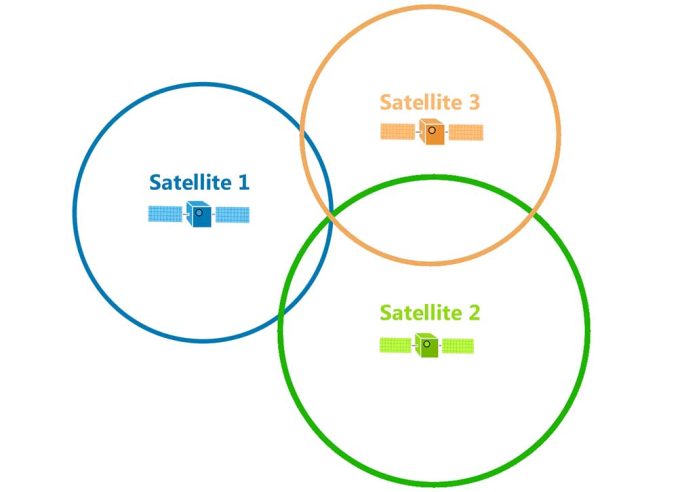
But the reality is in our three-dimensional world that GPS satellites broadcast signals as a sphere.
Each satellite is at the center of a sphere.
Where all spheres intersect determines the position of the GPS receiver.
READ MORE: GPS Accuracy: HDOP, PDOP, GDOP, Multipath & the Atmosphere
Triangulation Measures Angles, Not Distance
On the other hand, surveyors use triangulation to measure unknown distances. They do this by establishing a baseline length.
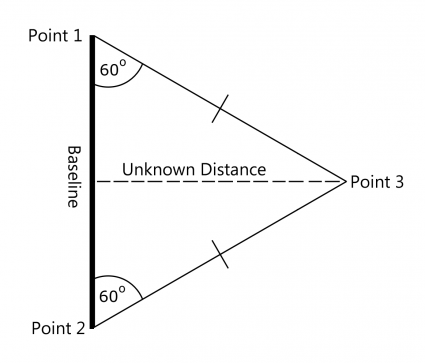
From each point, surveyors measure the angles of distant points using instruments such as theodolites. When we know the lengths and angles, triangulation determines the distances by forming triangles, as shown in the diagram above.
For example, surveyors gathered approximately 26,000 stations from Meade’s Ranch in Kansas to create the North American Datum of 1927 (NAD27). But the Global Positioning System uses the World Geodetic Survey (WGS84) to reference positions.
Conclusion
As GPS satellites broadcast their location and time, trilateration measure distances to pinpoint their exact position on Earth.
While surveyors use triangulation to measure distant points, GPS positioning does not involve any angles whatsoever.
Through the measurement of distances, your precise GPS location can be determined. Yet several factors such as HDOP, PDOP, GDOP, and the atmosphere can affect GPS accuracy and error.
GPS is a remarkable system for measurement and navigation like these 10 GPS apps. But do you want to learn more about satellites in orbit? Here are a few more articles to build on your expertise in the field:
- 15 Free Satellite Imagery Data Sources
- Geodesy: The Mathematics of “Where”
- The Big Satellite List. 50 Satellites. 30 Words or Less.
Hi, great explanation, one small part I’m not clear on. Could you possibly explain how a GPS devices calculates the distance to a satellite?
Joe, no you just need a receiver that can make some calculations. The position of the satellite is known because it’s floating in the vacuum of space in a very stable orbit. So using this information, you only need a small device to receive the clock signal from the satellite, and perhaps do some math accounting for the Doppler effect. From there you can calculate the origin of the spheres very accurately, and extrude them until they intersect with the spheres of the other satellites.
Using 3 satellites you can narrow down your GPS location to TWO points, to prove this, draw three circles that intersect each other, not touching the edges of each other. You’ll see that there are 2 intersecting points, adding a forth satellite will give you your true location and correct timing errors. The National Ocean Service U.S. Department of Commerce has a great explanation with pictures explaining this.
https://oceanservice.noaa.gov/education/tutorial_geodesy/geo09_gps.html
Very interesting. How can I find the WGS84 of a particular place? For instance an airport? Is there a database to search? Thanks for any help.
The time and space matters here. When the signal from the first satellite reaches the receiver, any point in the surface of the sphere is a possible location of the receiver. When a sphere of signal from the second reaches the receiver, it overlaps with the first sphere and narrows down the possible locations of the receiver to a circle (the overlap of two spherical surfaces). Now imagine only the circle’s boundary. When a signal of sphere from the third satellite reaches the same receiver, the overlap between the surface of the sphere and the circle from the previous satellites narrows the possibilities of the receiver’s location to just two points. One of these points is for sure the location of the receiver. Imagine only the two points now. when a signal from a fourth satellite reaches either of these points, we will know from elimination the exact point location of the receiver. Note that the location of these satellites are known with respect to Earth’s ground stations.
Trying to find the coordinates for the lowest elevation in the Western Hemisphere
The first part of the above example is true for 3 intersecting circles (a 2D world), but satellite signals represent spheres in a 3D world. This is vaguely explained further down in the article. Since GPS’s deal with spheres and not circles, a 4th satellite is needed to acurately determine one’s position. This 4th sphere is shown in the graphical picture, but really does not clearly represent why it is needed. Three spheres still leave an area of possible locations within the intersecting area. It is hard to represent this area visually. The fourth satellite or sphere pinpoints the exact location (without accounting for tranmission or timing errors). See this link to an image for a representation of the limits of 3 satellites. In addition to WAAS, more satellite signals help narrow down errors.
Kindly explain the reason why in satellite positioning observations must be made to a minimum of four satellites
It is required to determine correct position and time.
You just stated the reason. Could you explain it?
You need at least 24 satellites in orbit to have have 3 visible satellites at all times for triangulation.
I should elaborate, over the entire planet 24/7, I really don’t understand how this works, would you also need multiple ground stations?
Just curious you have 4 satellites covering half the globe, how many would you need to cover the entire globe, for … let’s say 24/7 communications?
Your explanation of trilateration is incorrect. Get someone who knows what they’re talking about to re-write the article.
What specifically is off about the explanation?