What is a Voronoi Diagram?
Voronoi Diagrams Find the Closest “Anything”
Imagine. You’re talking on your mobile phone…
Your network provider has a series of cell towers. When you make a call, which tower should your mobile phone connect to?
If all things are equal, the closest tower!
But how do you know what is the closest tower? It turns out that the answer lies in your Voronoi diagram.
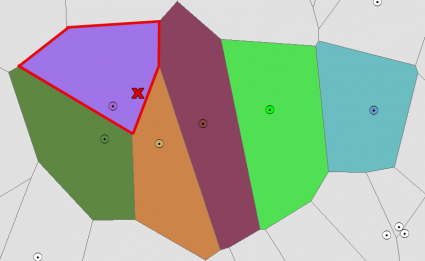
How to Interpret a Voronoi Diagram and Thiessen Polygons
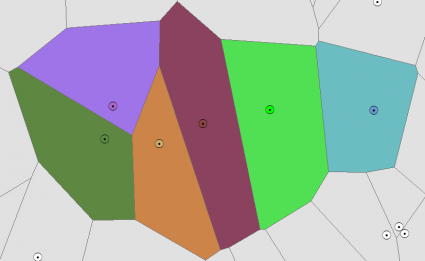
Let’s plot out a set of control points on a map. Each point has a specific color.
For every other pixel on the image, the Thiessen polygon takes the color of the nearest control point.
In other words, when you take a point in any given Thiessen polygon, it indicates that it’s closer to that generating point than to any other.
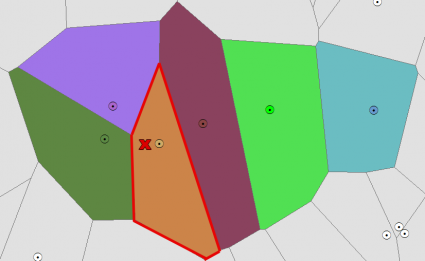
For example, if you walk in this Thiessen polygon of the Voronoi diagram, your mobile phone should connect to this tower highlighted in red.
This generating point is closest because the point is in this Thiessen polygon.
Likewise, when you walk over here, this is now the closest tower that it would likely connect to.
As a result, this illustrates a cellular coverage map. When you add a point anywhere on the map (entirely up to you), that is which cell tower their call will be routed to.
Pretty neat application of Voronoi Diagrams, don’t you think? Now, let’s create our own.
Let’s Make Our Own Voronoi Diagram
Now that you have an intuitive understanding of how a Voronoi diagram can be used, let’s make our very own.
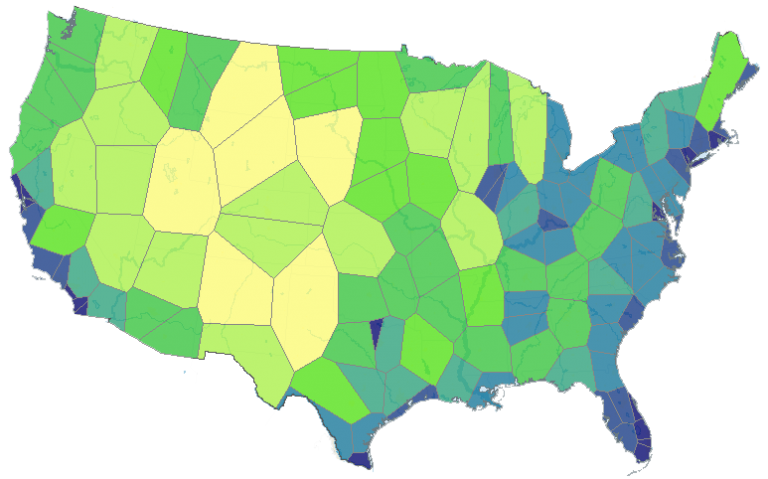
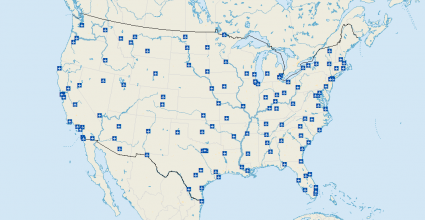
Here is the spatial distribution of airports in the United States:
In ArcGIS, select the Analysis > Proximity > Create Thiessen Polygons tool. After running the tool, here is the resulting Voronoi Diagram:
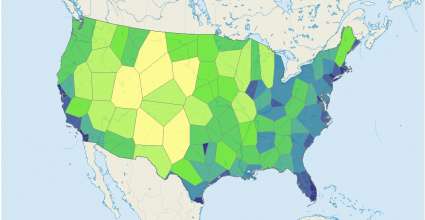
You can now see which airports are the most remote in the United States by the size of the Thiessen polygon.
Here is the World Airports Voronoi displaying how the airport on Easter Island (Mataveri Airport at 27°S, 109°W) is the most remote with the nearest airport about 2,600km away from it.
Now, It’s Your Turn
Voronoi diagrams are not just pretty pictures. As noted, they help understand the proximity and distance of features.
Georgy Voronyi is the creator of the Voronoi Diagram.
Consequently, his diagram is now being used in study areas like biology, networking, and geoscience.
What are some interesting applications of Voronoi Diagrams that you know?






“What are some interesting applications of Voronoi Diagrams that you know?”
We’ve traditionally built bridges and structures from trusses because beams are easy to manufacture, but in nature, trusses don’t exist, but voronoi patterns do. It’s nature’s “truss” essentially. Cellular Tissue forms in 2D and 3D voronoi patterns/volumes. Molds, fungi, Bone marrow, wings of insects, in stems and stalks of plants, heck, a honeycomb in a beehive is just a very specific type of voronoi pattern.
3D Printing as well, we are starting to see Voronoi 3D-printed casts instead of traditional plaster-poured casts. I mean, I guess we can’t even call it a cast any more because it’s not “cast” it’s printed/extruded. It’s just a limb-fracture ligature support or however you want to call it. Prosthetics and Bioengineered materials. No longer being limited by traditional manufacturing, like casts, forges, and milling, 3D printing allows man-made structures to have more optimized shapes determined by finite element solutions that end up looking like voronoi designs.
This is an example to illustrate a technique. It is for teaching purposes and not an optimal solution to any particular problem.
I understand why use it for cell towers. But why airports? If I would travel by car or public transport to “nearest” (fastest reached) airports wouldn´t quality and quantity of roads be very important parameter?