Conic Projection: Lambert, Albers and Polyconic

When you place a cone on the Earth and unwrap it, this results in a conic projection.

Some of the popular conic projections are the Albers Equal Area Conic and the Lambert Conformal Conic projections.

Both of these types of map projections are well-suited for mapping long east-west regions because distortion is constant along common parallels. But they aren’t the best at projecting the whole planet.

Here are some details on conic projections and how maps use them today.

Albers Equal Area Conic Projection

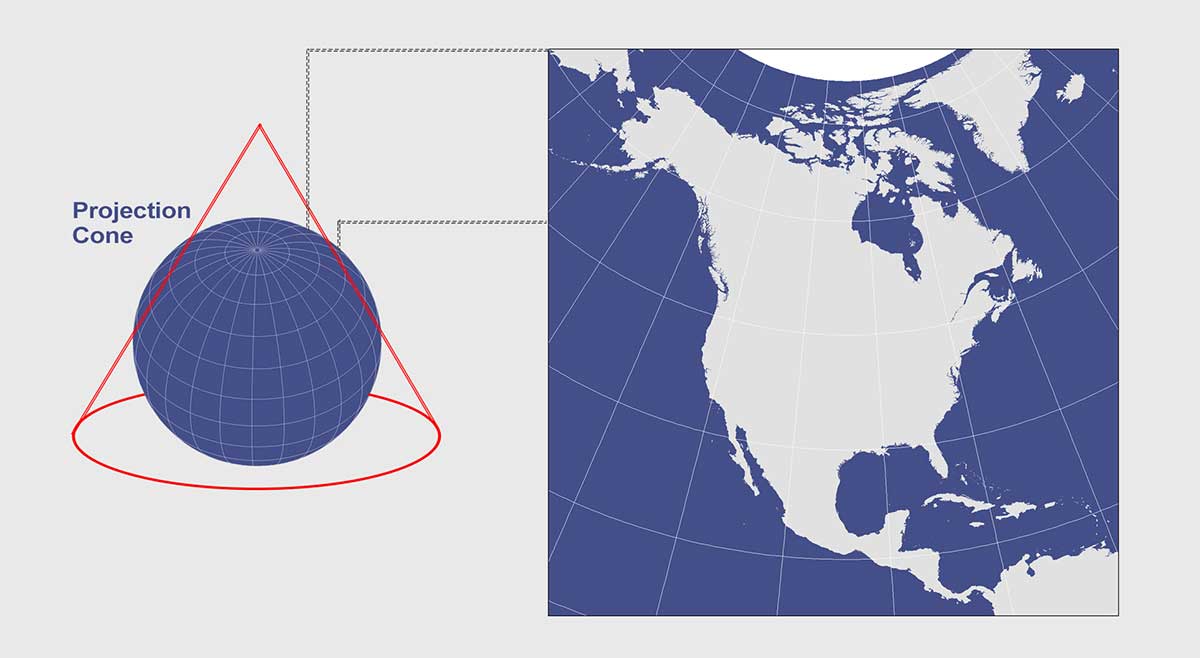
The Albers Equal Area Conic projection is commonly used for displaying large countries that require equal-area representation. For example, the USGS uses this conic projection for maps showing the conterminous United States (48 states).

H. C. Albers introduced this map projection in 1805 with two standard parallels (secant). As the name states, the purpose was to project all areas on the map proportionally to all areas on Earth. Like all projections, the Albers Equal Area Conic Projection has map distortion as shown in the table below.

Distortion	Description
Distance	True only on both standard parallels.
Scale	Distortion increases away from the standard parallels.
Direction	True direction is preserved along the standard parallels. Distortion in direction increases away from standard parallels.
Area	Accurate for areas near the standard parallels. Equal to the same areas on Earth, though it’s not conformal, perspective, or equidistant.

Lambert Conformal Conic Projection

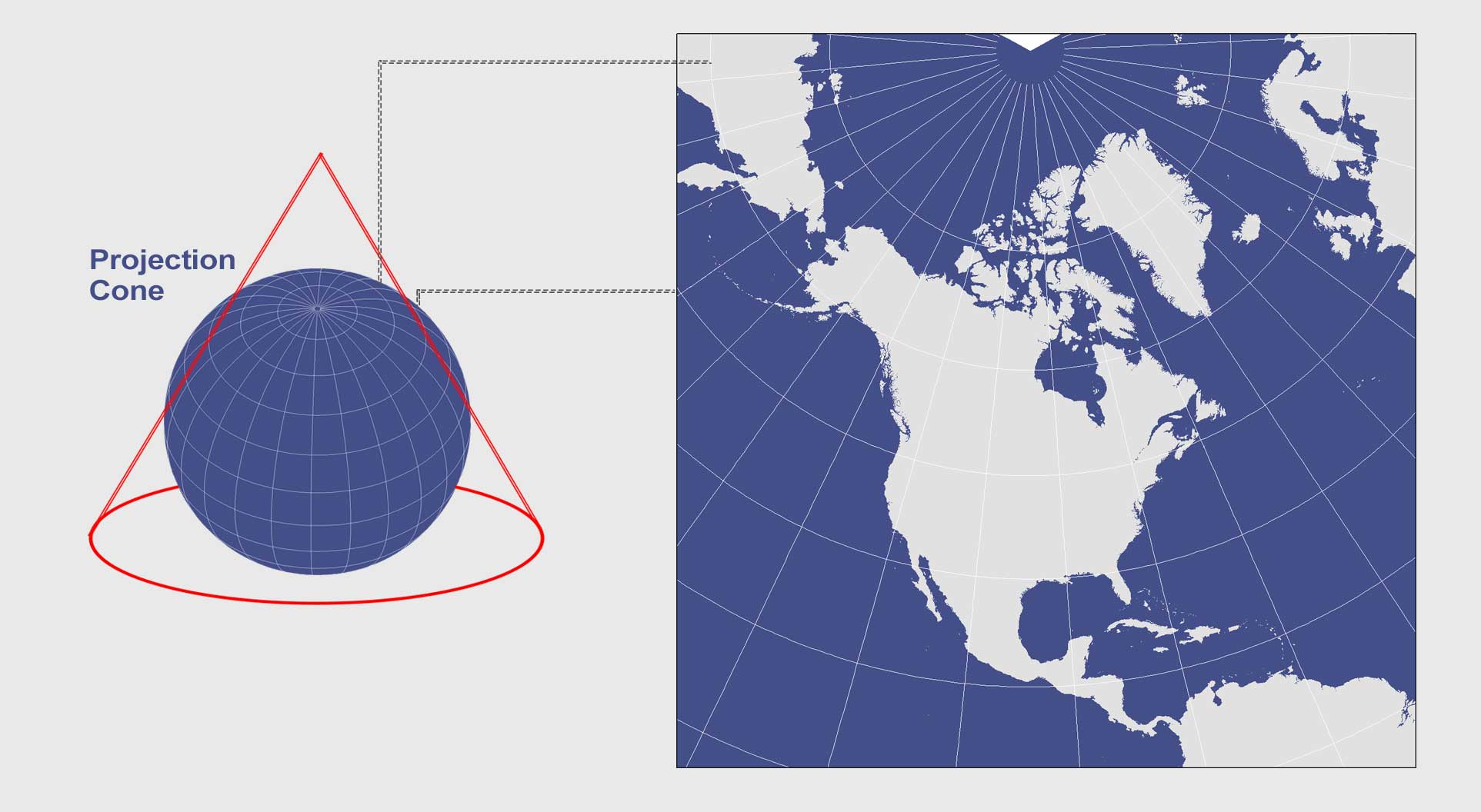
The Lambert Conformal Conic is one of the many creations by Lambert in 1772 still widely used in the United States today (such as in the State Plane Coordinate System (SPCS)). It looks similar to the Albers Equal Area Conic, but graticule spacings differ so that it’s conformal rather than equal area.

It uses a conic developable surface secant at two standard parallels, usually at 33° and 45° to minimize distortion. However, standard parallels vary depending on location. For example, Canada’s standard parallels are usually 49ºN. and 77ºN.

Distortion	Description
Distance	Distances are reasonably accurate and retained along standard parallels
Scale	Scale is constant along any given parallel.
Direction	True direction is preserved along standard parallels with distortion increasing away from standard parallels.
Area	It isn’t equal area as distortion increases away from standard parallels, especially near the poles

Polyconic Projection

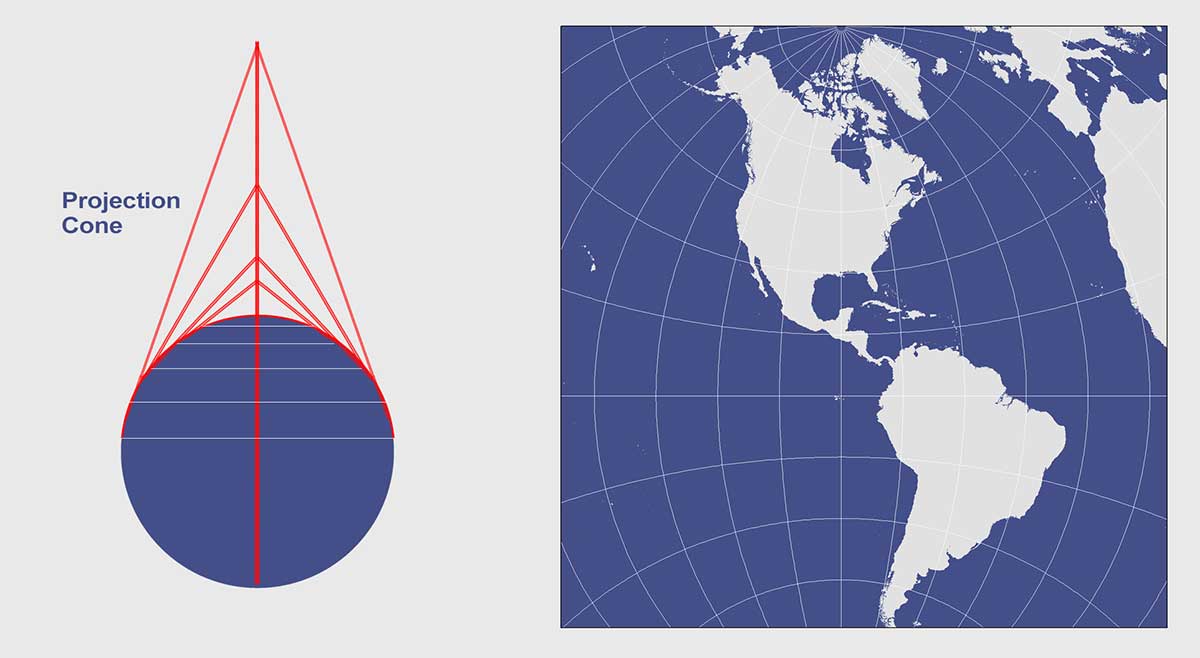
This now obsolete map projection uses an infinite number of cones tangent to an infinite number of parallels. This type of protection is generally used for countries that span along a longitudinal extent.

In a polyconic projection, all meridians except the central one have curved lines. Only along the central meridian, distances, directions, shape, and areas are true. However, distortion increases away from its central meridian. Overall, this map projection compromises many properties. It is neither conformal, perspective or equal area.

Distortion	Description
Distance	Distances are reasonably accurate and retained along standard parallels
Scale	Scale is constant along any meridian, but it increases away from the central meridian.
Direction	True direction is preserved along the central meridian and is distorted at the edges of the map.
Area	Distortion increases away from the central meridian. May be suitable for small areas and local mapping.

Conic Projection Advantages and Disadvantages

Unlike cylindrical maps, conic map projections are generally not well-suited for mapping very large areas. They are more suitable for mapping continental and regional areas. For example, Albers Equal Area Conic and LCC are common for mapping the United States.

Polar orientation conic projections have their cone center point directly above the pole. Meridians are straight converging at the pole. Parallels are arcs circling the pole. Parallels cross meridians at right angles.

Tangent cones result in one standard line where the scale on that line has no distortion. Secant cones cut distortion down with two standard lines. In general, these standard lines have no distortion but it increases away from these lines.