Cylindrical Projections in Cartography & Maps
Cylindrical Projection Examples
When you place a cylinder around a globe and unravel it, you get the cylindrical projection.
Strangely enough, you see cylindrical projections like the Mercator and Miller for wall maps even though they inflate the Arctic.
But it makes sense why navigators and even Google Maps use the Mercator projections – it’s all because of the unique properties of cylinders.
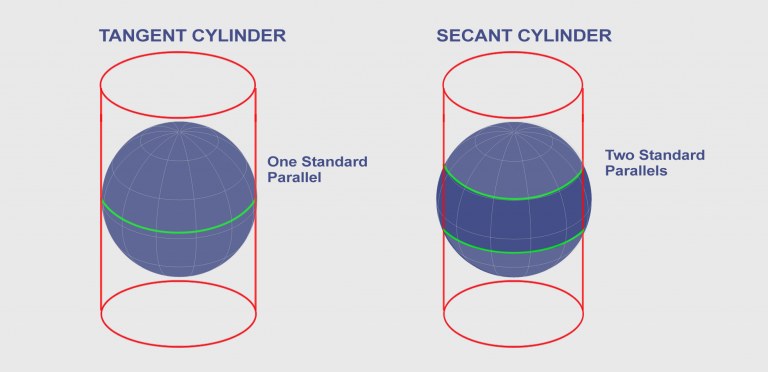
You can place it in a vertical, horizontal, or oblique position. Actually, the State Plane Coordinate System uses all these orientations.
So let’s look at some of these advantages and disadvantages. But first, let’s start with 3 examples of cylindrical projections.
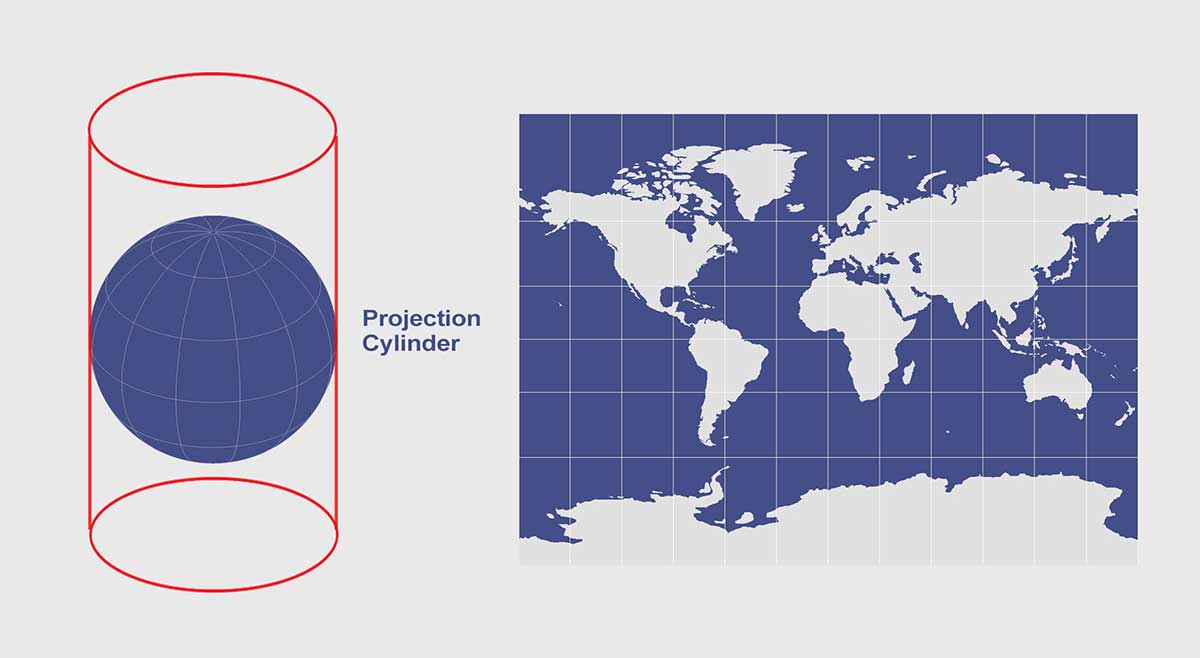
1. Mercator Projection
The legendary Flemish cartographer Gerardus Mercator created the Mercator projection by mathematically projecting a vertically oriented cylinder tangent to the Equator.
Navigators used this type of map because any straight line on a Mercator map is a rhumb line (line of constant direction). However, navigators often combined this type of map with the Gnomonic projection because of how straight lines are great circles showing the shortest path between points.
Mercator map projections show the true direction between places the best but are not equal-area or equidistant. This is the projection of choice from Google Maps for this reason, despite how the south and north poles distort land size.
Mercator Map Projection Properties
Directions along a Rhumb line are true between any two points on a map. Distances are true only along the Equator.
Although it has a conformal property, areas are greatly distorted increasing size at poles.
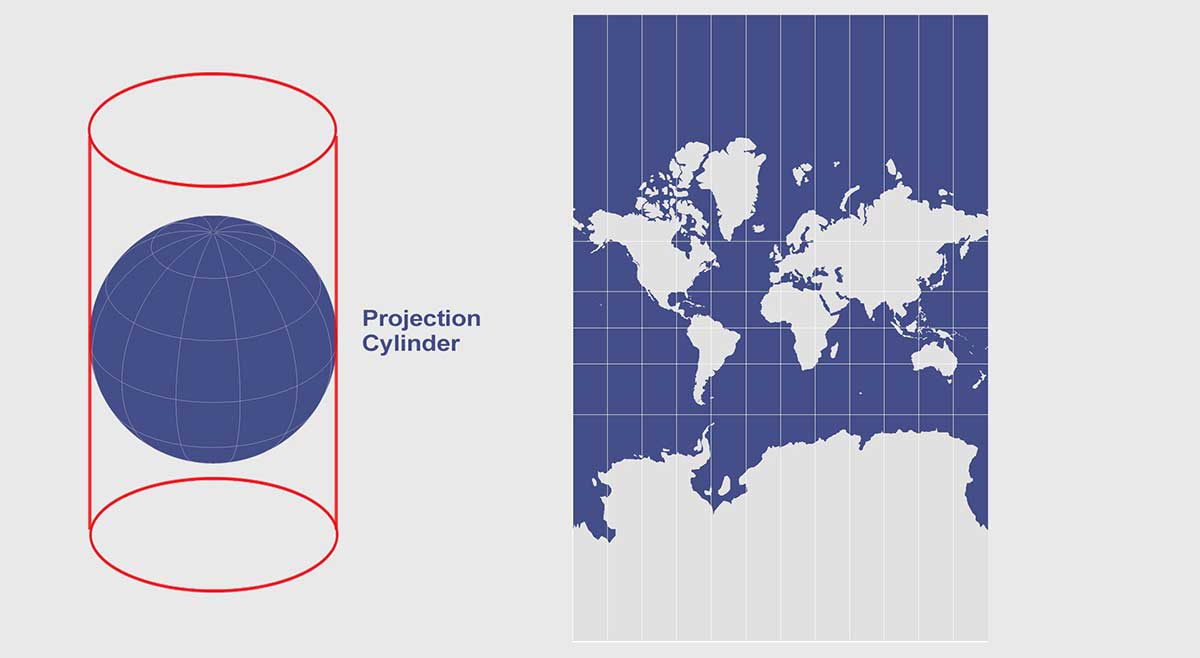
2. Transverse Mercator Projection
Lambert introduced the Transverse Mercator in 1772. It uses a horizontally oriented cylinder tangent to a Meridian. This is particularly useful for mapping large areas that are mainly north-south in extent.
The whole UTM grid system uses 60 horizontally oriented cylinders secant to the globe. While horizontal and vertical cylinders make up a Mercator and Transverse Mercator, an oblique aspect projection uses neither.
The USGS uses the Transverse Mercator in their 1:24,000 to 1:250,000 quadrangle maps because they can be joined at their edges. Further to this, State Plane Coordinate Systems use a Transverse Mercator when its orientation is a north-east extent.
Transverse Mercator Map Properties
Outside of a 15° band, distortion increases significantly for size, distance and direction. Distances are true only along the central meridian but all distances, directions, shapes, and areas are reasonably accurate within 15º of the central meridian.
The Transverse Mercator m projection is conformal with shapes being true in small areas. While the equator is a straight line, other parallels are complex curves concave toward the nearest pole.
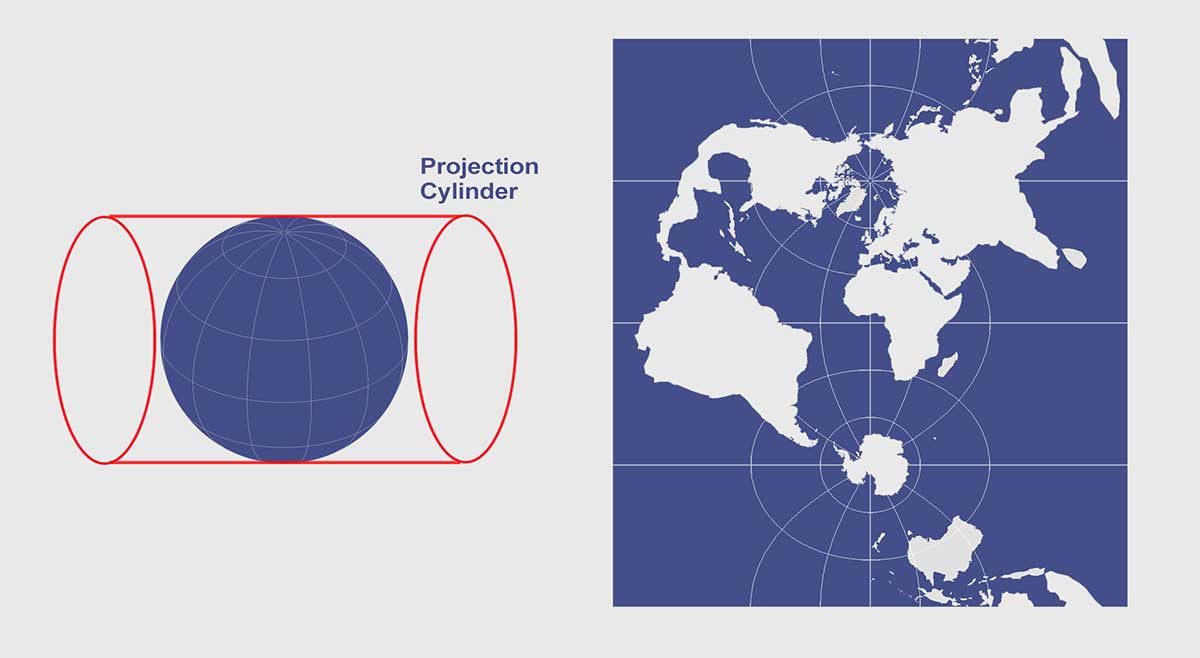
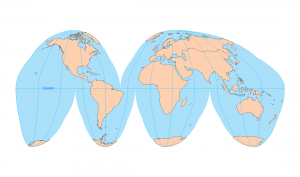
3. Miller Projection
It’s Miller time. The Miller Projection was developed by O. M. Miller in 1942 using a cylinder projection developable surface tangent at the Equator.
The Miller map projection is very similar to the Mercator Projection, but straight lines are not Rhumb Lines. This means that it’s not particularly useful for navigation, but more so for wall maps.
Poles are distorted without the same degree of bulging in the polar regions as the Mercator projection. This is why cartographers often use azimuthal projections for the polar regions. However, the Miller Projection increases the distortion of distances, areas, and shapes that occur at high latitudes.
Miller Projection Map Distortion
Area and shapes are still distorted, but not as extreme as the Mercator projection.

The Miller projection is a compromise projection, which means that it isn’t equal in area, equidistant, or conformal, and doesn’t sacrifice either one at extremes. Directions distortion increases further away from the Equator at higher latitudes.
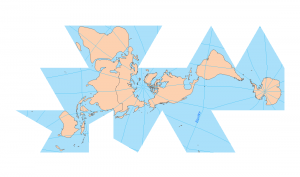
Pseudocylindrical Projections
The cylindrical family of map projections typically has equally spaced meridians to horizontal latitude lines.
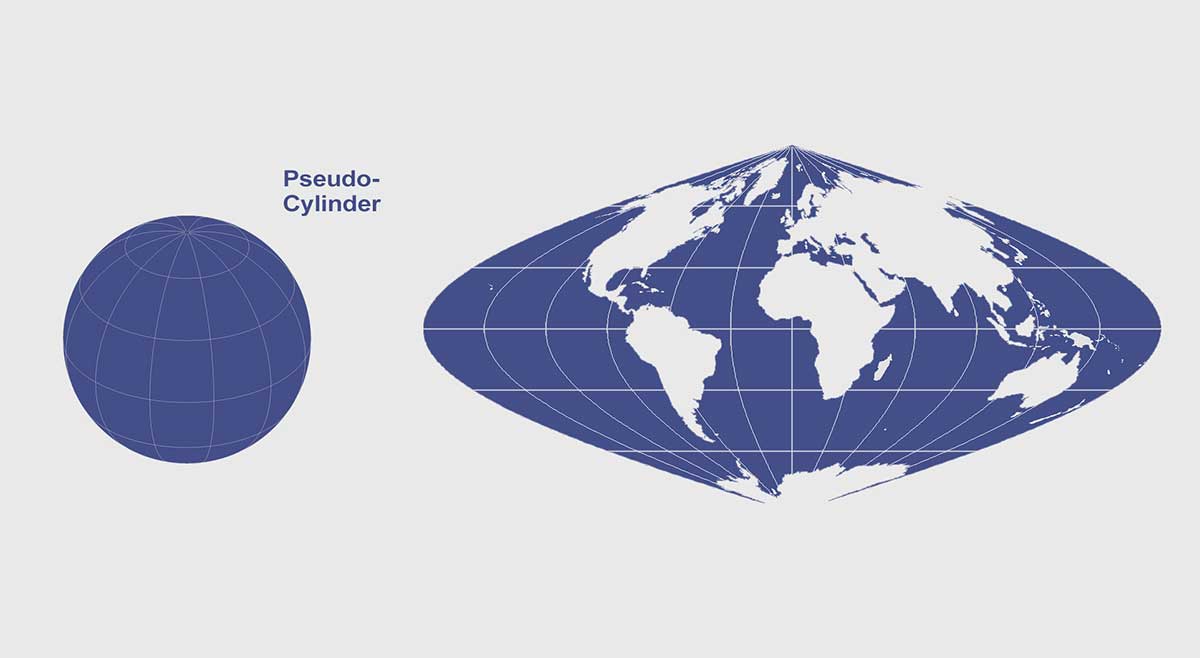
While the pseudocylindrical such as the Sinusoidal and Robinson projections have a central Meridian and horizontal parallels as straight line segments but not other Meridian lines.
For example, here is a Sinusoidal projection that uses a pseudocylinder.
Cylindrical Projection Advantages and Disadvantages
The globe is the only true surface where directions, distances, shapes, and areas are true.
A cylindrical projection does a fairly decent job of representing the entire globe, especially when you compare it with conic projections which are good for representing continents.
The Mercator projection is a popular choice for navigation because of how straight lines are Rhumb lines. The State Plane Coordinate System and UTM grids use a Transverse Mercator because it’s ideal for large-scale mapping when you use the correct zone.
Finally, compromise projections like the Miller projection take the best of all worlds without making a perfect equal area, conformal or equidistant map projection. Both secant and tangent cylinders minimize map distortion.





This article mentions (assumingly) Johann Lambert but does not make any attempt to explain who he is, simply referring to him as ‘Lambert.’ Who is this? What is his credibility?
No information about the shapes of Rhumb lines and Great circles.
Thank you so much! It was really helpful.
Really helpful