Why Are Rhumb Lines (Loxodromes) a Constant Track Direction?
Why Rhumb Lines are not the Shortest Path
When pilots want to fly in a constant track direction, they’ll follow rhumb lines (or loxodromes).
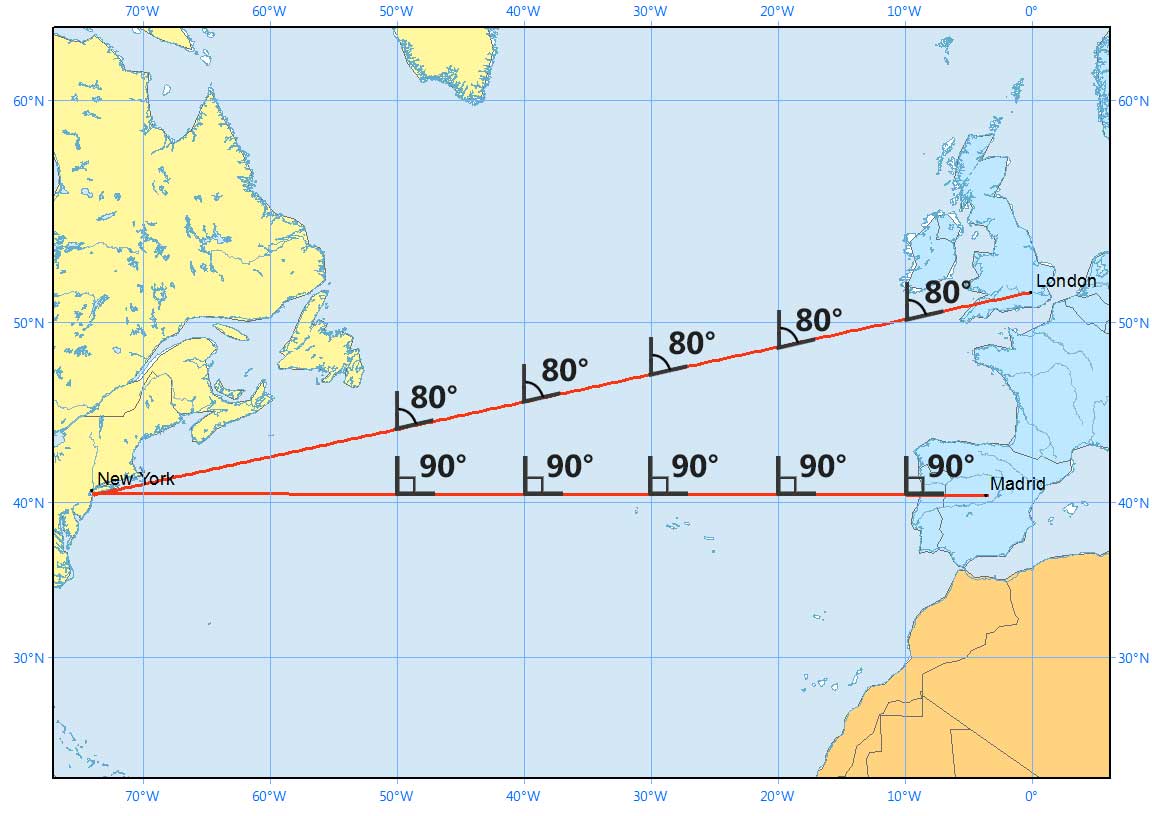
Rhumb lines have constant bearings and cross all meridians at the same angle.
Despite how rhumb lines look as if they are the shortest distance in certain map projections, they aren’t when traveling long distances on a sphere like the Earth. This is because the shortest distance is that of a great circle.
Now that you have a definition of a rhumb line, let’s look into it in a bit more detail.
Rhumb Lines on Map Projections
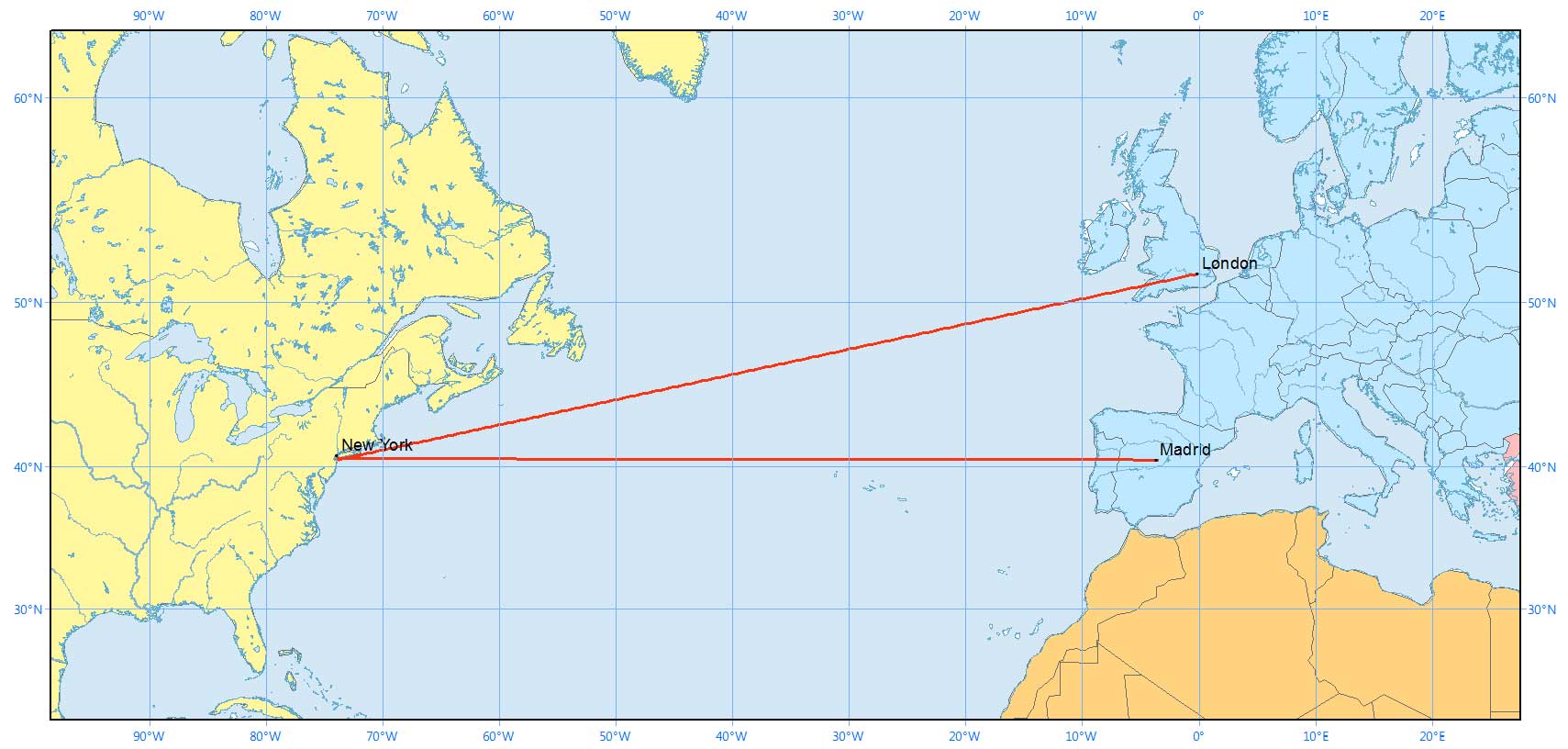
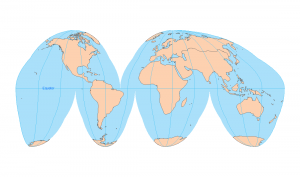
A rhumb line on a Mercator projection is a straight line. In the example below, two rhumb lines extend from New York to Madrid and London.
This is the reason why the Mercator projection is a popular map for sailors and pilots. Because the Mercator projection preserves angles and shapes (which makes the projection conformal), navigators can follow a single compass bearing resulting in a straight line.
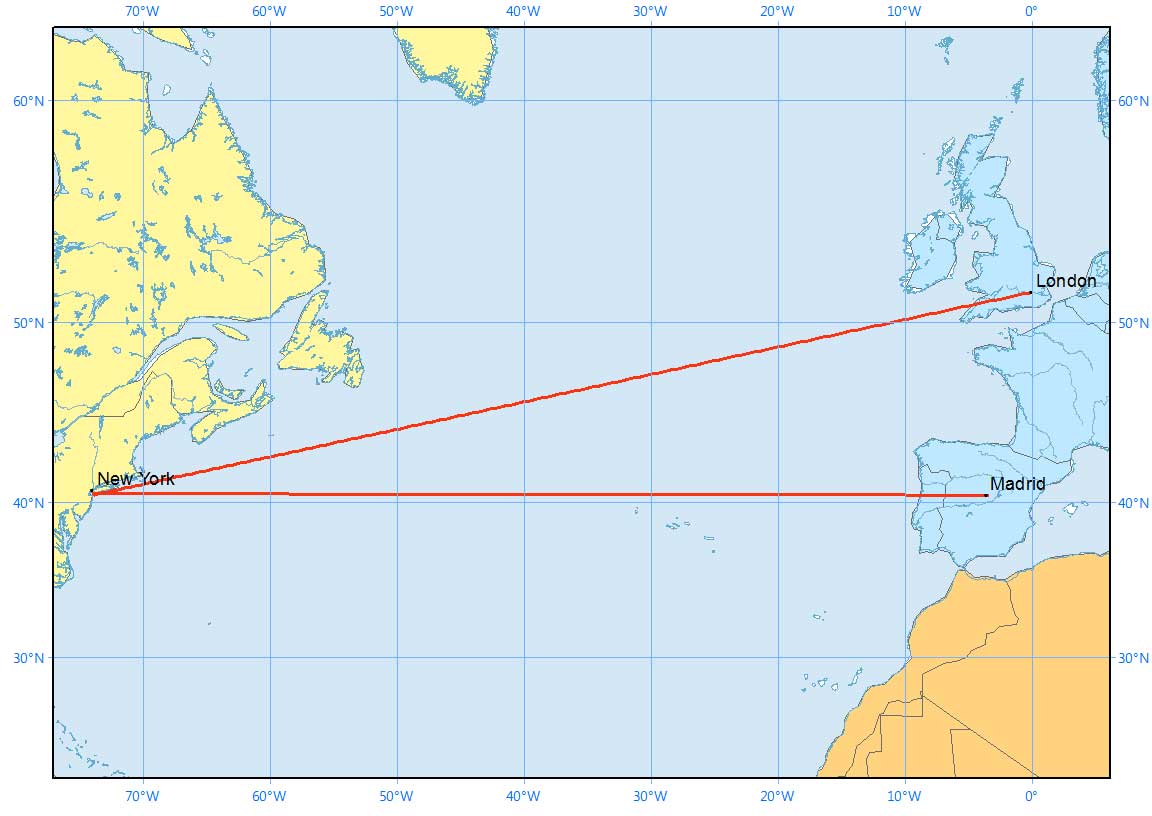
We illustrate a rhumb line cutting all meridians at the same angle in a Mercator projection below:
But what happens when you put the same rhumb lines in a different map projection?
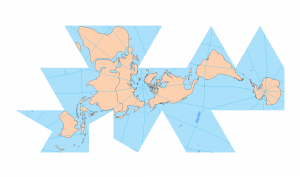
Here is how they look in the North Pole Azimuthal Equidistant map projection with a rhumb line to the North Pole. They look quite different, don’t they?
READ MORE: Map Projections: Flatten the Sphere
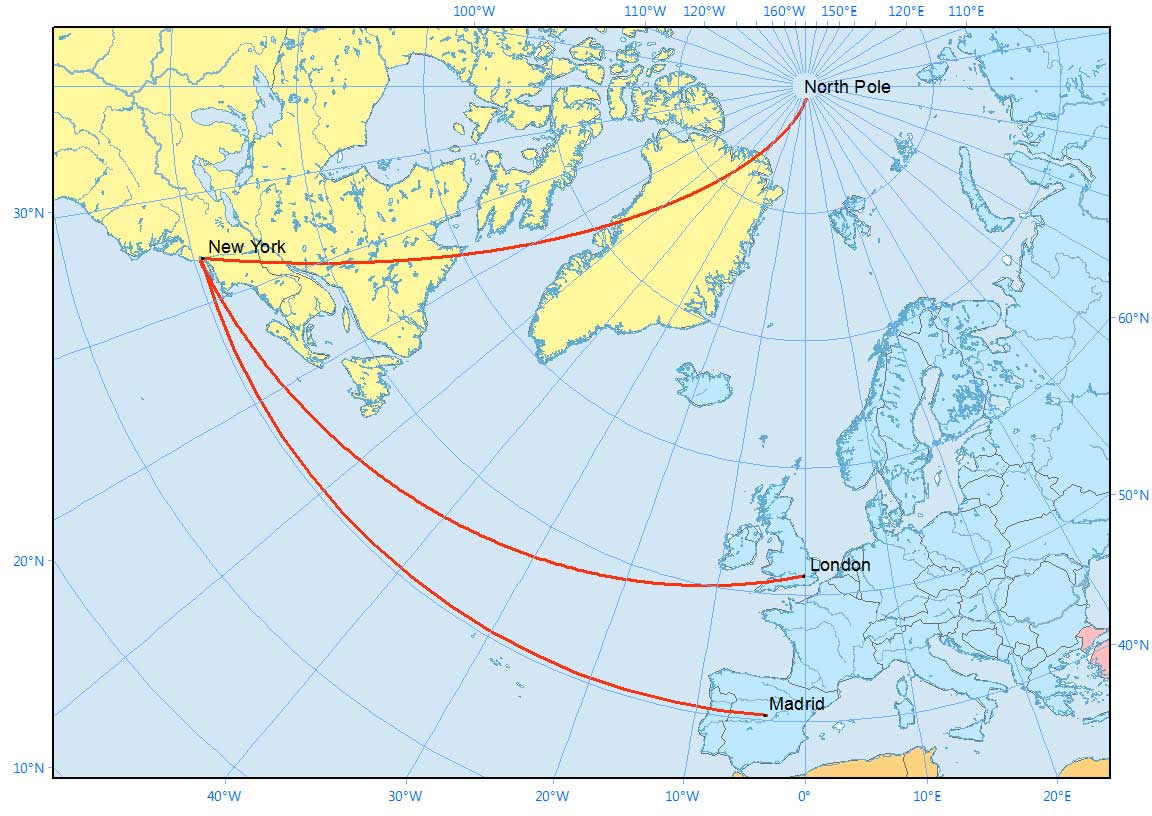
Rhumb lines appear on the surface of the Earth as a curved line concave to the nearer pole. These lines spiral on a polar projection but it’s because of the projection that it still crosses all meridians at the same angle.
During short routes, the difference in distance between rhumb lines and great circles is almost unnoticeable. One of the problems with navigating a great circle is the need for constant changes in the course direction. That makes rhumb lines a simple method for getting from A to B.
READ MORE: Great Circle: Why are Geodesic Lines the Shortest Flight Path?
Summary: What Are Rhumb Lines?
As an imaginary line on the earth’s surface, rhumb lines are a standard method of plotting a ship’s course on a chart.
However, a rhumb line is not the shortest distance between two points on a sphere. The shortest distance is called a great circle.
In mathematical terms, rhumb lines are called loxodromes from the Greek term for running at an inclined angle.
In the advanced toolbar in ArcGIS, you can construct these types of lines as geodesic lines. Try it out for yourself.





A rhumb line passes through the point of Tangency? yes or no
Nice explanation. I just dont get why the rhumb line in this example is being called concave. It is being bent outside of the pole, should that not be called convex??
Correction:
This is a beautiful explanation! It is short, and clear.
However, one of your lines on map 4 is incorrect. Both this map and the Mercator projection would have a straight line from New York City to the North Pole, like all the other meridians on both maps. (Meridians are halves of great circles, and are also drawn as straight lines on both maps.) This is one of two exception classes: a North/South rhumb line is along a great circle, as is any rhumb line along the equator. No other rhumb line is along a great circle path. Thus:
All rhumb lines not following the equator, or not following a meridian (N/S line) are not great circles, and are not the shortest path.
This also modifies the conclusion.
“However, a rhumb line is not the shortest distance…” is more accurately stated as:
“However, a rhumb line is RARELY the shortest distance…” Other fixes also work.
(If you make this change, straighten the line from NYC to the North Pole, explain the two exceptions, and change the concluding text to “rarely’, “not usually”, or another more accurate description, I will be grateful. I like referencing your clear work. Thank you!)