What is Bilinear Interpolation?
DEFINITION:
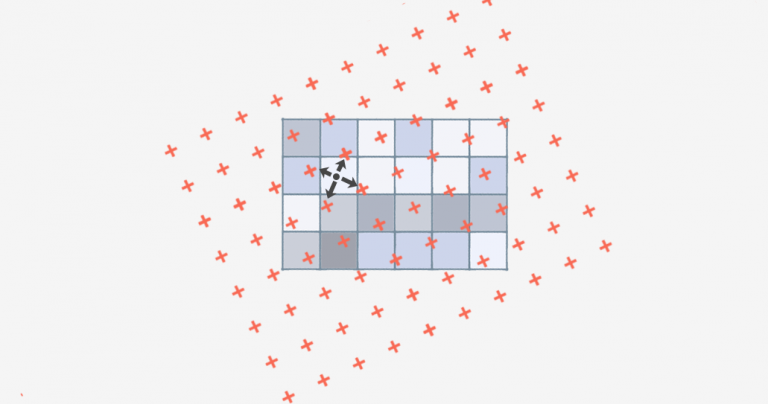
Bilinear interpolation is a method that estimates a value at a point between four known values on a grid, by using a weighted average based on both the x (horizontal) and y (vertical) directions.
Bilinear Interpolation in GIS
When you resample or reproject data, you may have to use bilinear interpolation (bilinear resampling) for your data.
The most common resampling operators are bilinear interpolation, cubic convolution, and nearest neighbor.
Today, we focus on bilinear interpolation, which estimates an output surface with 4 known values.
How is it different from the other interpolation techniques? Let’s take a look.
When Do You Use Bilinear Interpolation?
Before we do a full-depth explanation of bilinear interpolation, it’s important to know why you would use it in the first place.
Temperature gradient rasters, digital elevation models, annual precipitation grids, and noise distance rasters are all potential examples of when interpolation can be used to resample images. Each example has values that vary continuously from cell to cell to form a surface.
Here are a couple of examples of when you would use bilinear interpolation:
In both of these cases, you would use a resampling technique. Because when you have an input raster, how does the output raster know which cells to base the output on if the input cells don’t match?
You have to select a resampling technique such as bilinear interpolation, cubic convolution, or nearest neighbor.
How Bilinear Resampling Works
Bilinear interpolation is a technique for calculating values of a grid location based on nearby grid cells. The key difference is that it uses the FOUR closest cell centers.
Using the four nearest neighboring cells, bilinear interpolation assigns the output cell value by taking the weighted average. It applies weights based on the distance of the four nearest cell centers smoothing the output raster grid.
It’s recommended to use bilinear interpolation for continuous data sets without distinct boundaries. The surface must be continuous and the closest points must be related.
When you run the process, it generates a smoother surface, but not as severe as cubic convolution which uses 16 neighboring cells. The output raster will take only the four closest cell centers and apply an average using distance.
Why Use Bilinear Interpolation?
The key difference in bilinear interpolation is that it uses 4 nearest neighbors to generate an output surface.
On the other hand, cubic convolution uses 16 nearest neighbors which smooths the surface more so.
Bilinear interpolation assumes the input is continuous.
This resampling method uses a distance average to estimate with closer cells being given higher weights.

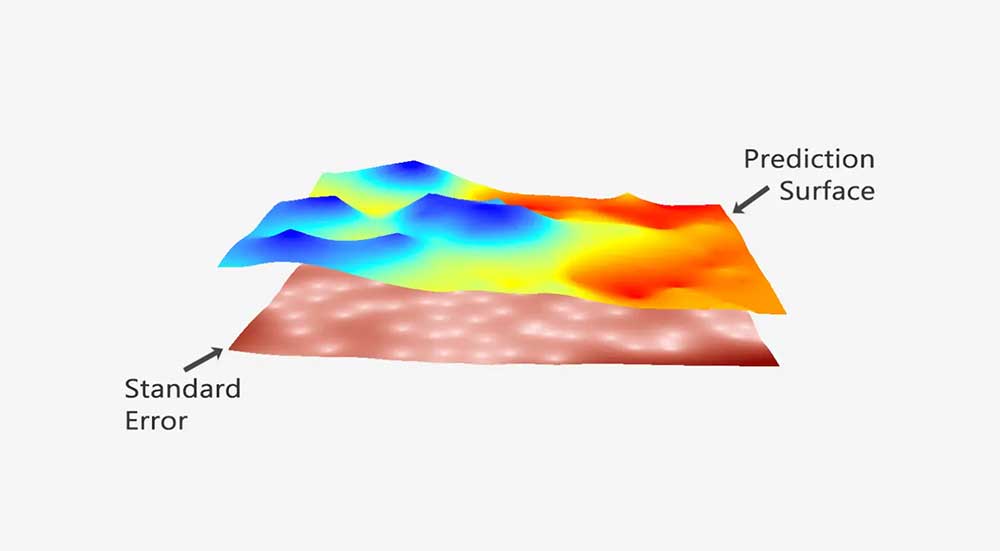









Recently I found an article wich recommended using “majority” techinique to alter the size of pixels in MDE rasters. What is your opinion about this? The article is this one: “Impacts of DEM resolution, source, and resampling technique on SWAT-simulated streamflow” written by Tan and collegues, 2015.
Nearest neighbor resampling often produced hillshades with stripes because the “nearest-neighbor” can produce adjacent pixels with identical values (hence striping). Bilinear interpolation can be used to minimize this hillshade artiticial stripes since a weighted average of the 4 nearest pixels typically produces different values in adjacent pixels.