How to Calculate Root Mean Square Error (RMSE) in Excel

Root Mean Square Error (RMSE) measures how much error there is between two data sets.
In other words, it compares a predicted value and an observed or known value. The smaller an RMSE value, the closer the predicted and observed values are.
It’s also known as Root Mean Square Deviation and is one of the most widely used statistics in GIS. Different than Mean Absolute Error (MAE), we use RMSE in a variety of applications when comparing two data sets.
Here’s an example of how to calculate RMSE in Excel with 10 observed and predicted values. But you can apply this same calculation to any size data set.
What is Root Mean Square Error (RMSE)?
For example, we can compare any predicted value with an actual measurement (observed value).
- Predicted value
- Observed value
Root mean square error takes the difference between each observed and predicted value.
You can swap the order of subtraction because the next step is to take the square of the difference. This is because the square of a negative value will always be a positive value. But just make sure that you keep the same order throughout.
After that, divide the sum of all values by the number of observations. Finally, we get an RMSE value. Here’s what the RMSE Formula looks like:
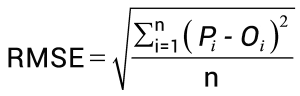
How to Calculate RMSE in Excel
Here is a quick and easy guide to calculating RMSE in Excel. You will need a set of observed and predicted values:
Step 1. Enter headers
In cell A1, type “observed value” as a header. For cell B1, type “predicted value”. In C2, type “difference”.
Step 2. Place values in columns

If you have 10 observations, place observed elevation values in A2 to A11. In addition, populate predicted values in cells B2 to B11 of the spreadsheet.
Step 3. Find the difference between observed and predicted values

In column C2, subtract the observed value and predicted value. Repeat for all rows below where predicted and observed values exist.
=A2-B2
Now, these values could be positive or negative.
Step 4. Calculate the root mean square error value
In cell D2, use the following formula to calculate RMSE:
=SQRT(SUMSQ(C2:C11)/COUNTA(C2:C11))Cell D2 is the root mean square error value. And save your work because you’re finished.
If you have a smaller value, this means that predicted values are close to observed values. And vice versa.
What’s Next?
RMSE quantifies how different a set of values are. The smaller an RMSE value, the closer the predicted and observed values are.
If you’ve tested this RMSE guide, you can try to master some other widely used statistics in GIS:
Or if you have any questions, please let us know in the comment section below.









How to get MAE from RMSE Data
You can’t. You need the raw data to calculate both MAE or RMSE.
This is so clear explanation of RMSE. Thanks a lot :)
Can we get a distribution of RMSE ? I think I need to know how to properly size the number of error measurements needed of a single design point so that I can have a way of calculating (or measuring) the RMSE at that design point.
How to interpret the result of RMSE?
Because you’re subtracting predicted with actual values… you can interpret it that the closer it is to 0, the closer actual values are to predicted values. That means a lower RMSE, the better or more accurate it is. I can’t think of a circumstance that this isn’t true.
What is the unit of MSE and RMSE in observed and satellite precipitation?
how to improve the RMSE?
Better predicted values that are closer to actual values
Can we use RMSE to compare land surface temperature from Landsat (predicted value) with surveyed measurment (observed value) of land surface temperature?
Yes, that is a good example of using RMSE
There is no need to create the C column, this Excel formula can calculate the RMSE from the A and B columns only.
=SQRT(SUMXMY2(A2:A11,B2:B11)/COUNTA(A2:A11))
can you calculate within arcmap ?
Hello,
How do you interprete the result of RMSE?
Hello,
How do we calculate the RMSE with GCPs. What would be the predicted value?
very good. thanks a lot.!!!!!!!