How Universal Transverse Mercator (UTM) Works
Universal Transverse Mercator (UTM) Projection
Start with a sphere or ellipsoid because that is the true form of the Earth.
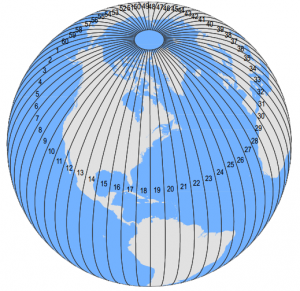
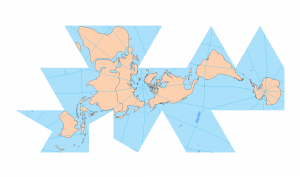
Then, peel it like an orange evenly into sixty segments called “zones”.
Finally, flatten each one of these zones.
What’s the result?
It’s the Universal Transverse Mercator (UTM) projection!
How Universal Transverse Mercator (UTM) works
It’s one of the most common map projections today. But how does the Universal Transverse Mercator work?
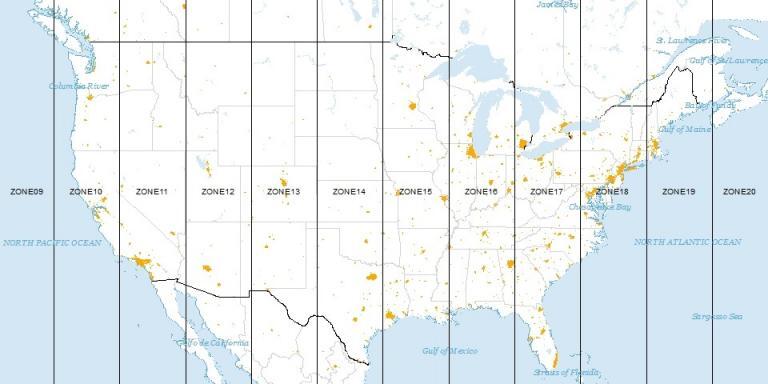
A UTM zone is a 6° segment of the Earth. Because a circle has 360°, this means that there are 60 UTM zones on Earth. (360 ÷ 6 = 60), right?
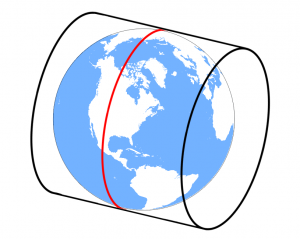
The Mercator uses an upright cylinder for its map projection. The Transverse Mercator takes a cylinder and places it on its side (rotates it 90°), as pictured below – which is how the term “transverse” is derived.
However, the Universal Transverse Mercator places this cylinder 60 times for each UTM zone.
This means that all 60 wedges are flattened out with a transverse cylinder. Each time it’s slightly rotated using a different meridian as a central line.
UTM applies a secant cylinder that intersects the ellipsoid along two small circles parallel to the central Meridian. This means that scale is constant north-south along the Meridians. But scale varies east-west along parallels.
The two small circles are 180 kilometers east and west of the central Meridian at the Equator. The small circles have a scale factor of 1, meaning a distance of 100 meters in the ellipsoid would be the same on the map projection.
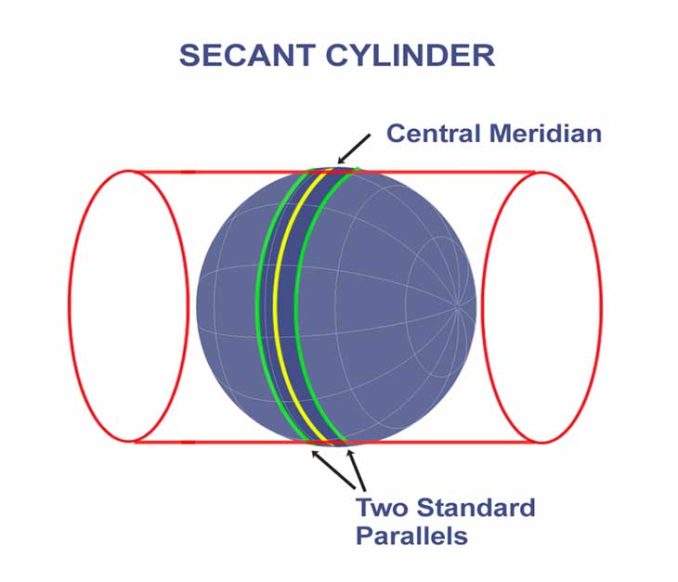
The centerline of a UTM grid zone has a scale factor of 0.9996. This means that a distance of 100 meters on an ellipsoid would be 99.96 meters on a map.
What is a false easting and northing?
Instead of using latitude and longitude coordinates, each 6° wide UTM zone has a central meridian of 500,000 meters. This central meridian is an arbitrary value convenient for avoiding any negative easting coordinates. All easting values east and west of the central meridian will be positive.
If you’re in the northern hemisphere, the equator has a northing value of 0 meters.
In the southern hemisphere, the equator starts at 10,000,000 meters. This is because all values south of the equator will be positive. This is called a “false northing” because y-coordinates in the southern geographic region will avoid negative values.
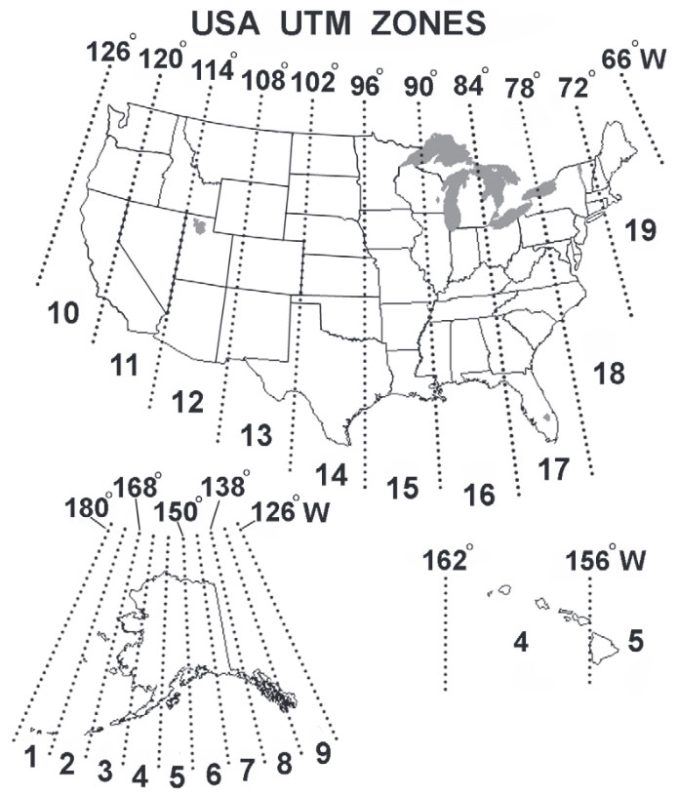
Which UTM zone do you live in? Because you’ll need a bit of a deeper understanding to specify the position of a point on Earth in that particular UTM zone.
For example, UTM Zone 17S will use a false northing with the equator starting at 10 million. The NAD 1983 UTM Zone 18N will have the equator start at zero meters.
If you have a set of UTM coordinates, you have to know which zone it is in beforehand. This is because the central meridian is assigned 500,000 meters in each zone.
UTM projection distortions
The UTM projection minimizes distortion within that zone. So this means that when you want to show features in several UTM zones, it starts becoming a poor choice of map projection.
Distortion is small near the central meridian, and as you move away it worsens. So this makes it most fitting for narrow regions and not well-suited for world maps.
Just like every map projection, the Universal Transverse Mercator has its strengths and weaknesses. It is up to the map-maker to determine what projection is most favorable for its purpose.
…The Universal Transverse Mercator was really meant to map features in one UTM zone at a time.
READ MORE: Map Distortion with Tissot’s Indicatrix
Flatten the Sphere 60 Times
The Universal Transverse Mercator (UTM) coordinate system is a standard set of map projections with a central meridian for each six-degree wide UTM zone.
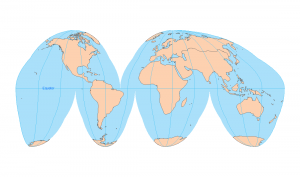
The transverse Mercator map projection is an adaptation of the standard Mercator projection which flips the cylinder 90 degrees (transverse).
The UTM projection flattens the sphere 60 times by shifting the cylinder central meridian 6° for each zone. This gives cartographers a map to work with always in meters.
The Universal Transverse Mercator is horrible for small-scale (less-detailed) maps like world atlases and perfect for mapping narrow regions.
There is no false easting.
Instead of a full six degrees in each zone. If you allowed for the distortion at the central meridian of 5.99678 degrees in each zone it would become less distorted.
Great to see this website. I think it is very useful for me
Why UTM coordinate system is not applicable beyond 84⁰N and 80⁰S
Those look like decimal degree coordinates (lat/long). Here’s more information on DMS and DD – Degrees/Minutes/Seconds (DMS) vs Decimal Degrees (DD)
Because the distance between two parallel and meridian is not constant value on pole. Besides this, the shape of the earth become flatten on the pole. This why cylindrical projection is not applicable for polar regions.
Why would UTM Zone 17S will use a false northing with the equator starting at 10 million? It’s clearly in the northern hemisphere.
The “secant cylinder” diagram shows a regular Mercator projection, with cylinder axis along the earth’s axis, both horizontal in diagram (UTM-Secant-Tangent-Cylinder-2-425×278.png). Transverse Mercator would keep the horizontal cylinder but have earth poles oriented up & down, as in the diagram before that one.
UTM system, because of the distortions in each zone, with movement away from the central merdian seems to be of limited use for cadastral and engineering surveying.
It is already known that it is not intended for small-scale mapping.
Why then is it being used by surveyors and allied specialists, while there are other projections -conical, orthogonal- and others.
How can we minimize the distortion of shape, area, distance and direction in UTM???
Take a look at compromise map projections. https://gisgeography.com/map-distortion-tissots-indicatrix/
UTM – Universal Transverse Mercator
What is the reason for the UTM projection to start on the antimeridian and not on the Greenwich meridian ????
Thank you
Yes. Since a UTM zone is a projection onto a strip of a cylinder, which is flattened out to a planar strip, grid north cannot be true north except at the central meridian. Consider this: For each zone, the central meridian passes through the North and South Poles. At any other point in that zone, a line PARALLEL to the central meridian MUST miss the poles; therefore at that point grid north has to deviate from true north. The amount of deviation increases with distance from the central meridian.
You did a good job of describing distance distortion.
I have not found any good references regarding direction distortion.
Is it true that grid north = true north at the centre of a projection, but not towards its edges?
Close, but not quite. There’s a few common misconceptions in this post that always need to be unlearned by students and practitioners.
First, the UTM System is not a projection (!!!); rather, it is a global system of narrow mapping zones – each with its own instance of the transverse Mercator coordinate projection method. 120 zones means 120 map projections.
Second, each instance of the transverse Mercator projection method used in this system is a secant type of projection (scale factor along the central meridian < 1.0) and not a tangent type (as illustrated above). Consequently, the distortion pattern created by each includes a swath of deflation between the standard circles, no distortion along the standard circles (scale factor = 1.0), and inflation beyond them.
TRY:
Distortion is small near the central meridian, decreases as you approach a standard circle, and then increases and worsens as you move beyond the standard circle and toward the edge of the zone.