Ellipsoid/Spheroid – Our Oblate Spheroid Planet Earth

We say Earth is a sphere. But it’s not exactly a perfect one.
It’s an oblate spheroid that bulges at the equator and is somewhat squashed at the poles.
In fact, it bulges about 14 miles out more at the equator compared to pole-to-pole.
Because of the field of geodesy, we’ve gained a much better understanding of the shape of our planet. Let’s delve into this a little deeper.
What is an Ellipsoid in GIS?
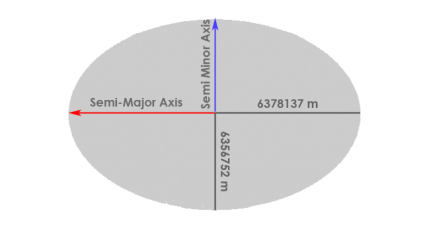
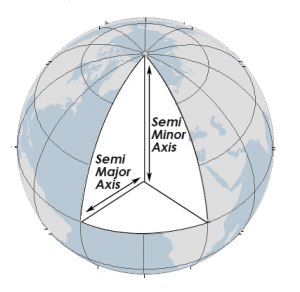
Geodesists have adopted an ellipsoid model to determine latitude and longitude coordinates. The major axis of an ellipse is the equatorial radius. The minor axis is from the poles to the center.
Geodesists use reference ellipsoids to specify point coordinates such as latitudes (north/south), longitudes (east/west), and elevations (height).
The most common reference ellipsoid in cartography and surveying is the World Geodetic System (WGS84). The Clarke Ellipsoid of 1866 was recomputed for the North American Datum of 1927 (NAD27).
When comparing NAD27 and NAD84, latitude and longitude coordinates can be displaced to the degree of tens of meters (with the same latitude and longitude coordinates). The image below shows an exaggerated semi-major axis and semi-minor axis.
How Do Horizontal Datums Relate to Ellipsoids?
Horizontal datums give us the capability to measure distances and directions across the surface of the earth. Most horizontal datums define a zero line at the equator from which we measure north and south (latitudes).
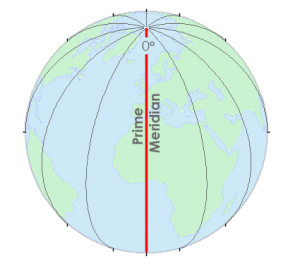
There is also a zero line at the Greenwich Meridian from which we measure east and west (longitudes). This standardized reference point simplifies navigation and geographic coordination, serving as a fundamental reference for global positioning and mapping systems.
Together these lines provide a reference for latitude and longitude expressed in decimal degrees. These latitudes and longitude positions (Geographic Coordinate Systems) are based on spheroid or ellipsoid surfaces that approximate the surface of the earth – a datum.
We reference all coordinates to a datum. This datum serves as a crucial baseline for establishing the accurate positions of geographic features and ensuring consistency in spatial data analysis and interpretation.
A datum describes the shape of the Earth in mathematical terms. A datum defines the radius, inverse flattening, semi-major axis, and semi-minor axis for an ellipsoid.
Here is the WGS84 datum:
- Semi-major axis: 6,378,137.0 m
- Semi-minor axis: 6,356,752.3142 m
- Inverse flattening: 298.257223563
| Name | Year | Semi-Major Axis (Equator Radius) | Semi-Minor Axis (Polar Radius) | Users |
|---|---|---|---|---|
| Clarke | 1866 | 6,378,206.4 m | 6,356,583.8 m | North America |
| International (Hayford) Ellipsoid | 1924 | 6,378,388.0 m | 6,356,911.9 m | Most of the World |
| WGS72 | 1972 | 6,378,135.0 m | 6,356,750.5 m | NASA |
| GRS80 | 1980 | 6,378,137.0 m | 6,356,752.3 m | Worldwide |
| WGS84 | 1984 | 6,378,137.0 m | 6,356,752.3 m | Current Worldwide |
Rotational Forces Flatten the Earth
Sir Isaac Newton proposed that the Earth flattens at the poles because of rotational forces. As the Earth spins on its axis, the centrifugal force causes the Earth to bulge out at the equator. This is why the Earth is better modeled as an ellipsoid, which is a sphere slightly flattened at the poles.
In the 19th and 20th centuries, different ellipsoids were adopted in various parts of the world. Surveys were being performed on different continents. Each survey produced different ellipsoidal parameters.
For example, surveys in Australia yielded the “best” ellipsoid, which was different from South America and Asia. There wasn’t a unifying global ellipsoid. Each continental survey was isolated with its own ellipsoid parameters.
There was no clear way to combine these global survey measurements. There was a scarcity of survey points in specific areas and a lack of computational resources that prevented a global ellipsoid.
Fitting the Ellipsoid with the Geoid
A horizontal coordinate system gives us our latitude and longitude. On the other hand, a vertical datum is another component of your typical horizontal coordinate system.
We are on a three-dimensional planet that has ups and downs in addition to the side-to-side in a horizontal coordinate system on the surface. To handle the ups and downs, we have the vertical datum which gives a place to put zero measurements. Mean sea level is often understood as the basis for our ups and downs. This is called the geoid.
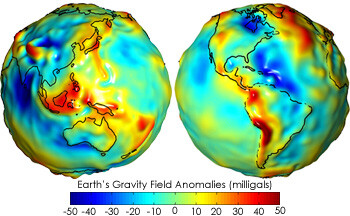
Vertical datums are lumpy and irregular. This is because of the varying densities in the Earth in different places. There are gravity anomalies such as mountainous areas having more mass.
This means that the mean sea level is not as smooth as everyone thinks it is. Geoids are not constant and they differ from place to place. They have undulations as you move around on the Earth.
The Earth is not as round as we like to pretend it is. We have lumps or undulations on them as they come back to us in the form of a geoid. The geoids put the lumps back into our nice smooth horizontal datum coordinate system.
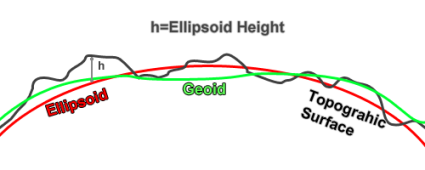
Ellipsoid height is the most basic version of up-and-down. The ellipsoid uses the size and shape of the horizontal datum such as WGS84. It gives a smooth surface without bumps or irregularities. The geoid describes it mathematically. Therefore, we fit different Ellipsoids to approximate it such as WGS84.
The Varying Historical Accuracy of the Ellipsoid
Earth bulges out more at the equator than at the poles by about 70,000 feet. Since the beginning of the 19th century, scientists have repeatedly calculated the dimensions of the ellipsoid with considerably different accuracy.
The early attempts at measuring the ellipsoid used small amounts of data and did not represent the true shape of the Earth. In 1880, the Clarke ellipsoid was adopted as a basis for its triangulation computations.
The first geodetic datum adopted for the United States was based on the Clarke ellipsoid with its starting point in Kansas known as Meade’s Ranch… and now we have geocentric datums like WGS84 and NAD83 with their major and minor axis.





The Alaska DNR requested I convert NAD27 to NAD83 (2011) to do land recombination to subdivided land on Wrangell Island (know between 12 August 1881 to 29 July 1901 as New Columbia Land. Then I was advised by Lt. Owen and Dr. Dennis at NOAA that both Wrangell Island and Saint Paul island in Alaska never had extended NAD27 to them, so 178^31’W longitude was not fixed by NAD27. An inquiry with the NGA came up with the fact that 1505 NR1, 2-1 in 1966 used Hayford of 1910. Can one convert the 178^31’W longitude from Hayford Ellipsoid to NAD83 (2011)?
I’ve done dozens of land surveys with my Dad who is a surveyor and engineer.
We’ve done rails to trails topo surveys over 75 miles. Never adjusted to any curvature because there isn’t any! And no, our instruments didn’t adjust either. How can you adjust for curvature when nobody even agrees with the actual shape of the earth?
That includes the professionals messaging back and forth on this website.
There are no actual photos of earth from space. Only CGI. NASA admits this claim.
For Ayebare Mary, this links to information about the Earth Gravitation Model of 2008.
https://earth-info.nga.mil/GandG/wgs84/gravitymod/egm2008/egm08_wgs84.html
As for the field of study most associated with geoid modeling and gravity, it is geodesy, specifically physical geodesy. Geophysicists also contribute.
A good, accessible text on geodesy is: Geodesy for Geomatics and GIS Professionals by Elithorp and Findorf (citation from memory).
There are more rigorous texts as,well,as lecture notes and reports at The Ohio State University and University of New Brunswick to name two.
The value for the inverse of flattening you report for the WGS84 datum is wrong.
The inverse of flattening is:298.257223563 NOT the value you show.
The semi-minor axis (b) you show for WGS84 truncates the official value in NIMA TR 8350.2 third edition. The value is 6356752.3142 meters.
As you know, truncating values impacts results using them. The significant figures used in the Technical Report are intended to insure agreement in numerical results. As the semi-minor axis is NOT a defining parameter, it is computed using a and f. Given a and b one can also compute the flattening or its inverse.
To Derrick Chella
The following site run by the US National Geodetic Survey can perform these conversions for either single of multiple points in the US:. https://geodesy.noaa.gov/NCAT/
In the section “What is an ellipsoid in GIS” you show more of a circle than an ellipsoid. You also show the semi-major axis as larger than the semi-minor axis. Your illustration does not bring the semi-major axis back to the spin axis.
Your article also shows incorrect WGS 84 parameters for both b and 1/f. They should be:
Semi-minor axis (b) 6356752.3142
Inverse of flattening should be: 298.257223563
Strictly speaking both the WGS 84 and GRS80 reference ellipsoids are defined by
Semi-major axis (a)
Earth gravitational constant (GM)
Angular velocity of the Earth (mu)
Reciprocal of flattening (1/f)
Retired geodesist
Thanks, it’s updated
Okay thanks but I need to know the earth gravitational models
I think I understand the concept of a Geoid representation, but I don’t understand why the Geoid image looks lumpy – when you look at an image of Earth from space, it looks “smooth” and basically spherical (Even if we know it isn’t actually a perfect sphere)
I’m curious as to what branch of science this subject falls under? Looking for textbooks on Amazon on cartography shows books that focus more on aesthetics, and not many of them.
I’d say it falls under geomatics. Here’s a brief explanation on the topic – https://gisgeography.com/geodesy/
I would like to convert latitudes/Longitudes into northings and eastings which software can I use.
You can use QGIS, which is completely open source.