What is Map Algebra? [Raster Math]

What is Map Algebra (Raster Math)?

Map algebra basically involves doing math with maps.

But the key difference is that it only applies to raster data. That’s why we also call it raster math.

First, let’s review the different types of map algebra. Then, let’s practice with an example.

This video provides examples using arithmetic and relational operations with the raster calculator in ArcGIS Pro.

Types of Map Algebra

As you’ve learned, map algebra uses math-like operations. For example, you can apply simple math like addition or multiplication to update raster cell values.

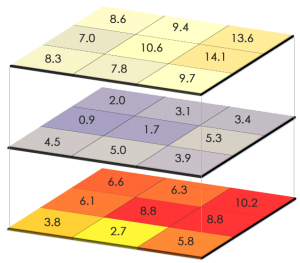
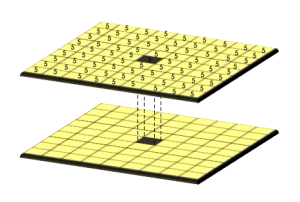
The most common type of map algebra is a cell-by-cell function. This type has rasters directly stacked on top of one another. Then, the function applies to cells aligned with each other.

But you can also change the configuration so it’s not only cell-by-cell. Here are the types of map algebra operations that you can use:

Let’s review how each type works.

Upgrade your raster skills

How To Mosaic Raster Datasets

Least Cost Path Analysis in GIS

1. Local Operations

The simplest approach is using map algebra on a cell-by-cell basis. For example, you have 2 rasters stacked on top of each other. Then, you add each cell one by one.

If raster cells represent temperature, you can subtract them both at different time periods. By using a local operation, you can find the difference in temperature for each cell.

2. Global Operations

Global operations apply a bulk change to all cells in a raster. If you want to add a value of 1 to all grid cells, this is a global operation.

For example, Euclidean distance is an example of a global operation. By calculating the closest distance away from a source, it applies the function globally in a raster.

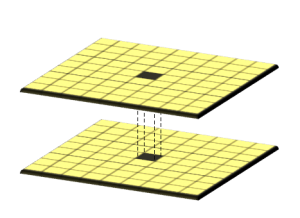
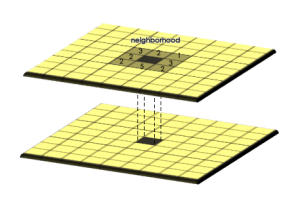
3. Focal Operations

Focal operations are spatial functions that compute an output value of each cell using neighborhood values. For example, convolution, kernel, and moving windows are focal operations.

MOVING WINDOW: A moving window is a rectangular arrangement of cells that shifts in position. Applying an operation to each cell from a moving window smooths values in a raster.

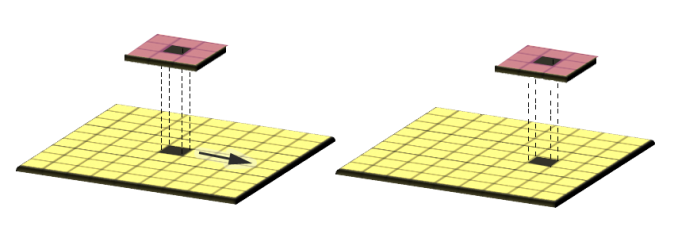
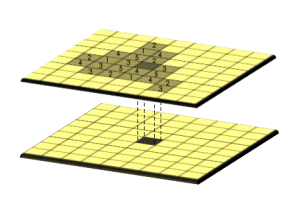
4. Zonal Operation

Zonal operations apply a math function to a group of cells within a specified zone. For example, a zone could be a vector or raster format.

If you want to find out how much rain is in a watershed, you can use a zonal operation. By using a raster with precipitation, you can set your zone as a watershed with a sum function.

Mathematical Functions

Here are examples of operations that you can use for map algebra:

Map Algebra Example

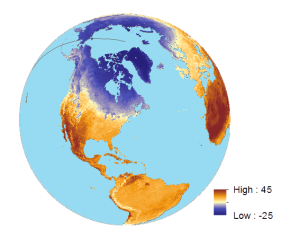
If you were to take a snapshot of land surface temperature in April 2015, it would look like this:

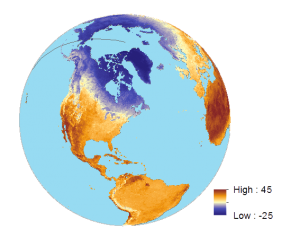
Then, if you took the April 2014 land surface temperature, here’s what it looks like:

When you subtract April 2014 from April 2015 for land surface temperature, it shows the difference between temperatures for two given periods.

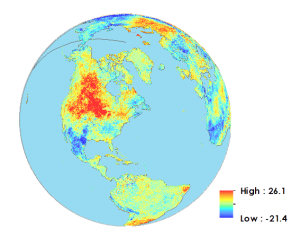
This is an example of a local operator because it subtracts each cell from one year to another. It’s also an example of an arithmetic operator because it uses subtraction.

Cells overlap with a range of -25° to +45°C. Then, we subtracted 2014 from 2015 land surface values for each cell. As a result, the output map has a range from -40° to +40°C.

What’s special about this is that you can pinpoint cells with the greatest difference. If values are positive, this means that 2015 land surface temperatures were hotter. But if values are negative, this means that 2015 land surface temperatures were colder.

What happens when you have null values? Null isn’t a numerical value. If there are null values in any of the raster cells, they will remain null in the output raster.

Map Algebra in ArcGIS Pro

You can use map algebra in ArcGIS Pro in either the “Spatial Analyst” or “Image Analyst” tools. Remember that you’ll need any one of these license types to use the tool. In ArcToolbox > Spatial Analyst Tools > Map Algebra > Raster Calculator.

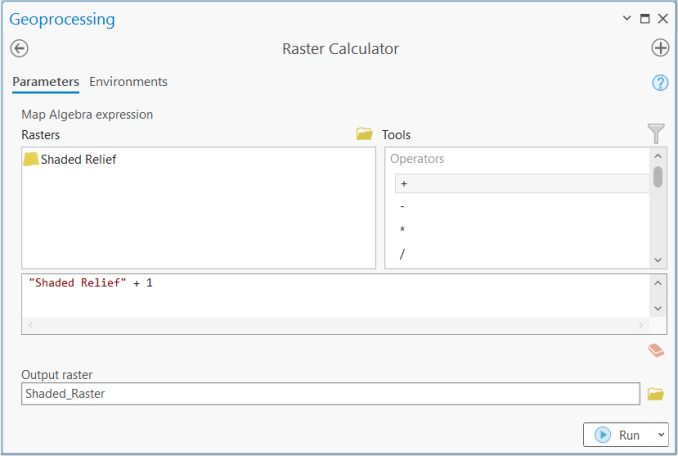
Now, let’s get hands-on experience using the raster calculator in ArcGIS Pro:

Here some of the different types of operators that you can use.

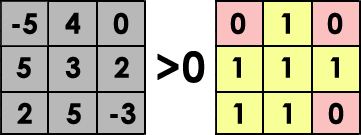
Relational Operators

Relational operators are logical functions that test a relationship. For example, here are operators that test logic:

Examples of relational operators are:

If it’s true, it returns a value of 1. But if it’s false, then it returns a value of 0.

Statistical Operators

Statistical operators calculate statistics for each cell by using statistical functions. For example, minimum, maximum, average, or median are statistical operators.

You can really crunch numbers using tools like zonal statistics. This tool uses a statistical operator to evaluate numbers for all cell values within a zone.

For example, zonal mean, median, and minimum are tools that use statistical operators.

Data Citation

Land Surface Temperature Data provided by NASA’s Earth Observatory Team, using data provided by the MODIS Land Science Team.