What is Tobler’s First Law of Geography?

Tobler’s First Law of Geography

Everything is related to everything else. But near things are more related than distant things. This is the first law of Geography introduced by Waldo R. Tobler in 1969.

This law suggests that objects or phenomena that are geographically close to each other are more likely to be similar or have some kind of spatial relationship compared to objects that are farther apart.

For example, this concept applies to pollution, noise, soil sciences, and countless phenomena. Here are some more examples of the first law of Geography.

---

Everything is related to everything else, but near things are more related than distant things.

Waldo R. Tobler

---

Example 1. Store Locations

An example of Tobler’s First Law of Geography can be seen in economic activities. Let’s consider the distribution of retail stores in a city.

According to Tobler’s law, stores that are located close to each other are more likely to have similar customer demographics, purchasing patterns, and even types of goods sold.

This is because customers in a specific neighborhood are more likely to visit nearby stores due to convenience and accessibility, leading to shared characteristics among stores in close proximity.

In contrast, stores located in distant neighborhoods might serve different customer segments, offer different products, and exhibit variations in business performance due to differences in demographics, local preferences, and accessibility.

Example 2. Semivariograms as Graphs

If you look 1 meter ahead, the terrain elevation is very likely to be the same. When you look 5 meters ahead, the ground elevation is going to be a little less similar. But it may start to vary. Now, when you look 100 meters away, elevation varies more to the point that they aren’t related.

We use semi-variograms in kriging interpolation to understand patterns related to distance. Semi-variograms take 2 sample locations and denote the distance between points as h.

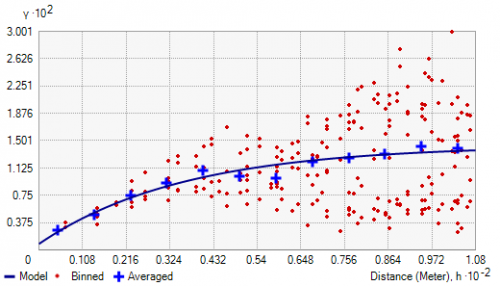
The x-axis plots the distance (h) between points. It groups distance by lags. Based on pairs, it measures the variance between the response variable (on the y-axis) and the distance between those two points on the x-axis.

As distance increases, the response variable becomes less predictable and is less related. But for closer things, the response is more predictable and has less variability. Overall, semi-variograms show Tobler’s First Law of Geography by graphing a variable by distance.

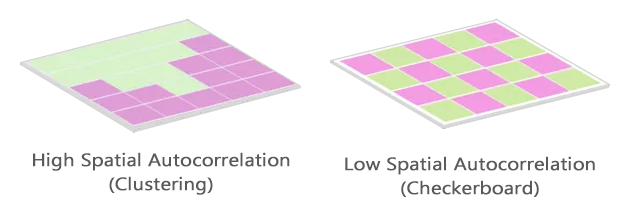
Example 3. Spatial Autocorrelation and Moran’s I

We can describe Tobler’s First Law of Geography numerically with autocorrelation. Spatial autocorrelation helps understand how similar closer objects are to other nearby objects. Moran’s Index (or simply Moran’s I) measures spatial autocorrelation.

We classify Moran’s I as positive, negative, and with no spatial auto-correlation.

Positive spatial autocorrelation indicates similar values cluster in a map. But negative spatial autocorrelation indicates dissimilar values cluster in a map. A value of 0 for Moran’s I typically indicates no autocorrelation.

Using spatial autocorrelation, geographers understand whether or not diseases and other phenomena are isolated. Moran’s I can imply the phenomena is spreading with dispersion or clustering.

The First Law of Geography

Tobler’s First Law of Geography is based on cost distance or distance decay. This means there is a greater hindrance to two places farther apart.

For example, people are less likely to travel a greater distance to visit a store as shown in Huff’s Gravity Model.

As distance increases, the greater the hindrance to transportation costs and purchases.

Now, bonus points to anyone who can describe the lesser-known Second Law of Geography. Let me know in the comment section below.