How Map Projections Work
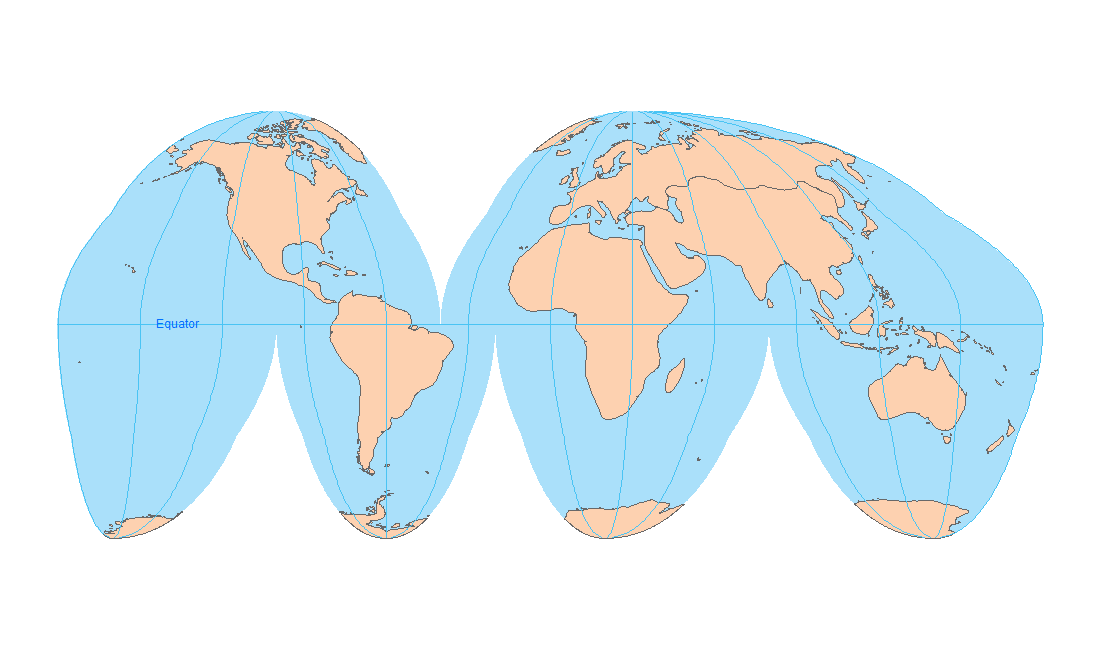
What are Map Projections?
Earth is a big blue marble that’s the shape of a sphere (or close to it). This is why a globe is the best way to represent the Earth.
But globes are hard to carry in your suitcase and you can only see one side of the globe. On top of that, it’s hard to measure distances and they’re just not as convenient as paper maps.
This is why we use map projections on globes and flatten them out in two dimensions. But as you’re about to find out, you can’t represent Earth’s surface in two dimensions without distortion.
On top of that, all types of map projections have strengths and weaknesses preserving different attributes.
Peel an Orange and Flatten the Peels

Imagine you have an orange. This is your imaginary Earth. When you look at it in any direction, you won’t be able to see all sides of it. But when you peel the orange, flatten and stretch it out, you can begin to see everything.
Similarly, a map projection is a method by which cartographers translate a sphere or globe into a two-dimensional representation. In other words, a map projection systematically renders a 3D ellipsoid (or spheroid) of Earth to a 2D map surface.
There are multiple ways to represent a sphere on a two-dimensional surface, as you can see in this Map Projection Transition Visualizer.
Because you can’t display 3D surfaces perfectly in two dimensions, distortions always occur. For example, map projections distort distance, direction, scale, and area.
Every projection has strengths and weaknesses. All in all, it is up to the cartographer to determine what projection is most favorable for its purpose.
Developable Surfaces in Map Projections
As you’ve already learned, map projections are fundamental tools in cartography that aim to depict the Earth’s three-dimensional surface on a two-dimensional map.
To achieve this, mapmakers utilize various mathematical techniques to transform the Earth’s curved surface onto different geometric shapes known as developable surfaces. For example, these surfaces include cylinders, cones, and planes.
The goal of a developable surface is to flatten the world in a two-dimensional plane. Each surface is mathematically rendered based on those geometric shapes.
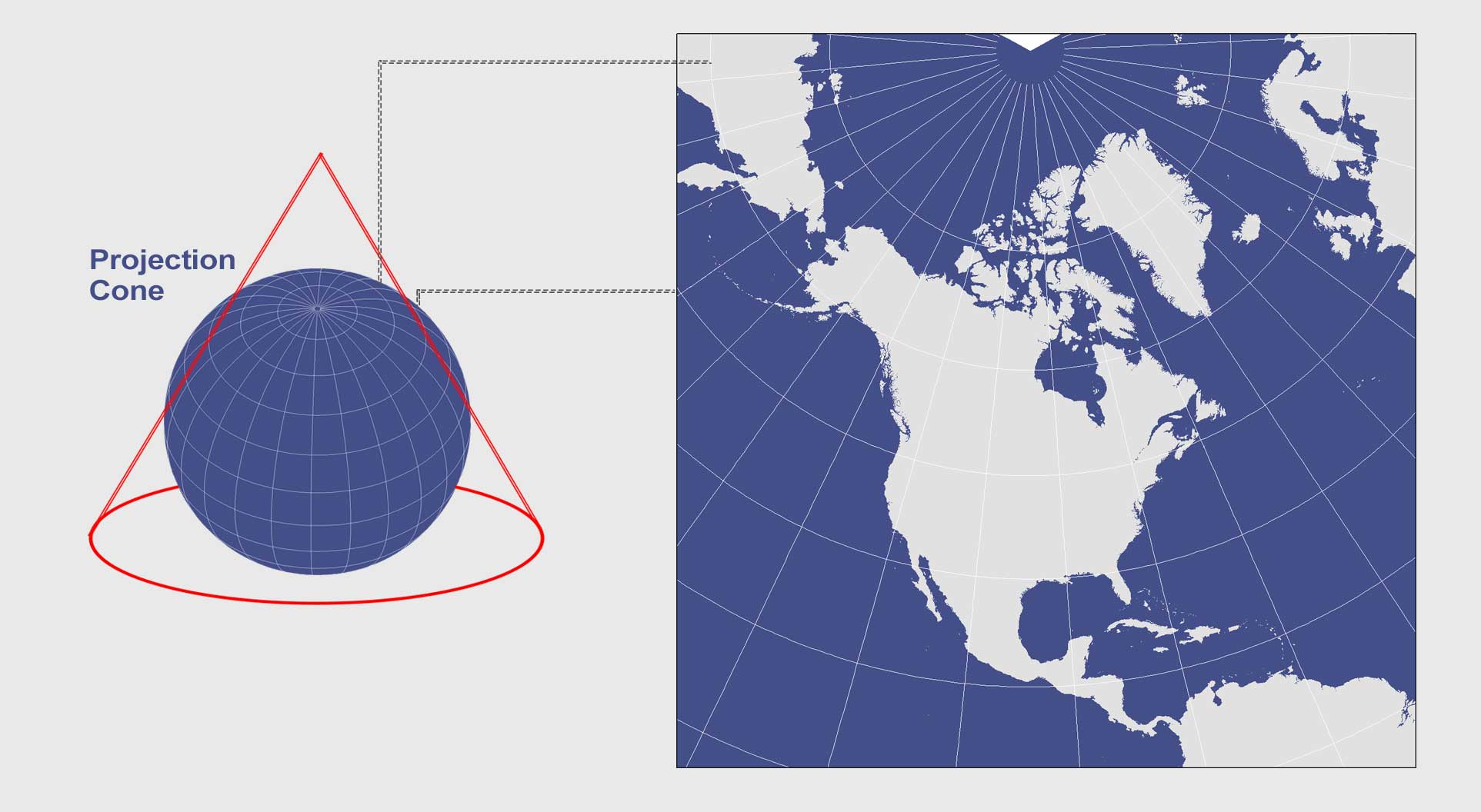
Conic Projections
When you place a cone on the Earth and unwrap it, this results in a conic projection. For example, the Albers Equal Area Conic and the Lambert Conformal Conic projections are conic projections.
Both of these map projections are well-suited for mapping long east-west regions because distortion is constant along common parallels.
But they struggle at projecting the whole planet. While the area is distorted, the scale is mostly preserved. For conic map projections, distance at the bottom of the image suffers with the most distortion.
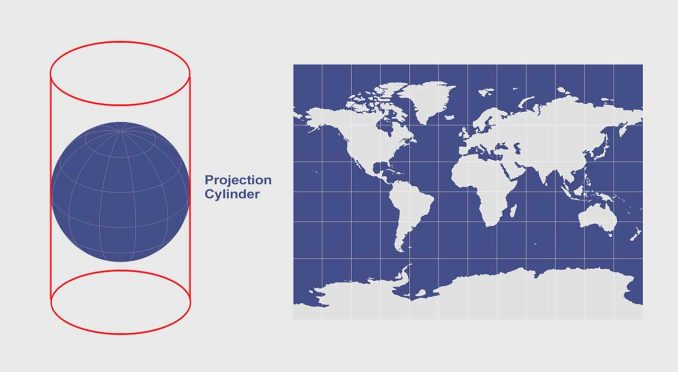
Cylindrical Projections
When you place a cylinder around a globe and unravel it, you get the cylindrical projection. Strangely enough, you see cylindrical map projections like the Mercator and Miller for wall maps even though they inflate the Arctic.
But it makes sense why navigators and even Google Maps use the Mercator projections – it’s all because of the unique properties of cylinders and north always facing up.
You can place it in a vertical, horizontal, or oblique position such as the State Plane Coordinate System. Each one has its own use in mapping the world.
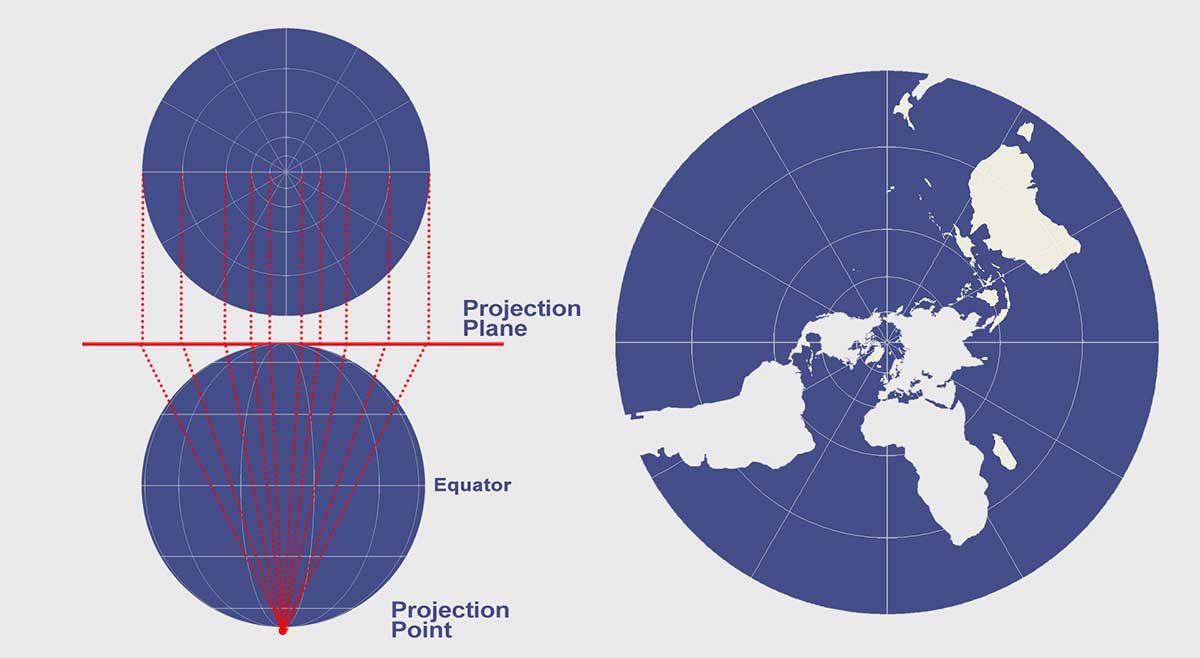
Azimuthal Projections
These types of projections plot the surface of the Earth using a flat plane. Similar to light rays radiating from a source following straight lines, those light rays intercept the globe onto a plane at various angles.
The light source can be emitted from different positions developing different azimuthal map projections. For example, gnomonic, stereographic, and orthographic are common azimuthal projections.
Map Projections and Coordinate Systems
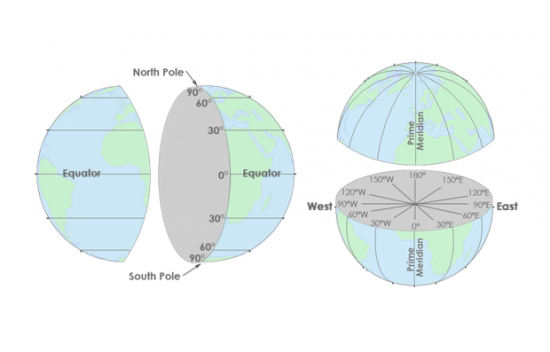
Remember that with a sphere, we use latitude and longitude to pinpoint our position. This is our geographic coordinate system. For example, New York’s position is (40.714°, -74.006°).
But when the Earth has a map projection, this means that it has projected coordinates. For example, the Universal Transverse Mercator system splits the Earth into 60 sections by lines of longitude. If you can imagine you are cutting an orange into 60 wedges, this is how the UTM system works.
From here, it assigns the central meridian a value of 500,000 meters.
The key takeaway is this:
When we locate positions on a sphere, we use decimal degrees. But when we use map projections, we locate positions in meters or feet.
It uses an equation to transform Earth’s angular geographic coordinates to XY Cartesian coordinates using developable surfaces. A developable surface is a geometric shape that a map projection can be built on.
Actually, some map projections don’t use developable surfaces at all such as the Goode and Bonne projections.
Examples of Map Projections
Throughout human history, people have used map projections for a wide range of uses. Explorers use Mercator maps for rhumb lines to accurately travel in a constant track direction. Actually, the first known map originated in Greece and perceived the world as cylindrical.
There are thousands of map projections that are in existence today!
Some map projections are useful for some things and other map projections are good for other things.
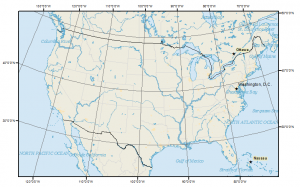
Two of the most common map projections used in North America are the Lambert conformal conic and the Transverse Mercator.
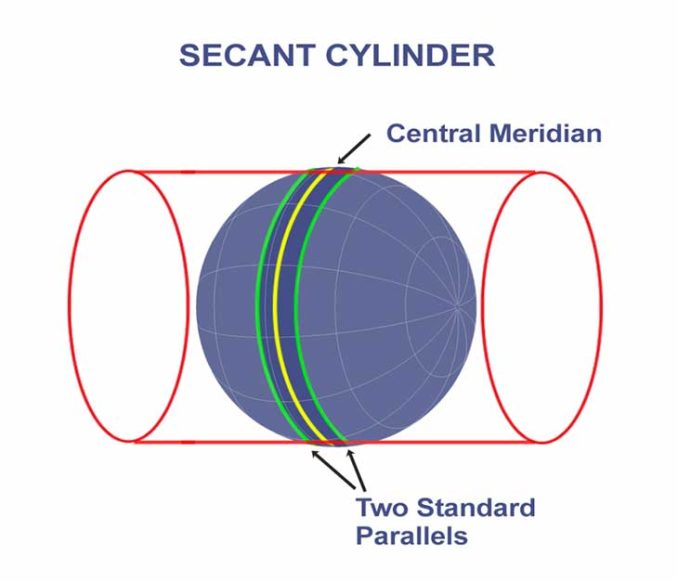
Lambert Conformal Conic
The Lambert Conformal Conic is derived from a cone intersecting the ellipsoid along two standard parallels. When you “unroll” the cone on a flat surface, this becomes the mathematically developed surface.
The most distortion occurs in the north-south directions. In general, distortion increases away from the standard parallels. For example, this map projection severely expands South America.
Universal Transverse Mercator
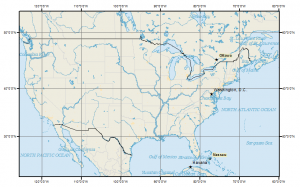
The Universal Transverse Mercator (UTM) coordinate system is a standard set of map projections with a central meridian for each six-degree wide UTM zone. Even though Google Maps used the Mercator projection because it preserves shape decently, and north is always up.
But Mercator map projections are really bad at preserving area. For most of us, the projection is common enough that it looks fine. In reality, Africa is huge on the globe. But Greenland appears to be as large as Africa, even though in reality it is only 1/14th the size. The Mercator puzzle game illustrates this point.
What is Your Favorite Map Projection?
Spatial referencing systems (latitude and longitude) are used to locate a feature on the Earth’s spheroid surface. The location of any point on Earth can be defined using latitudes and longitudes. These points are expressed in angular units such as degrees, minutes, and seconds.
Most maps in a GIS are in two-dimensional form. To make use of these maps, you need reference systems that use a pair of coordinates.
However, when you transfer a spherical shape to a flat surface, you approximate the true shape of the Earth. Depending on the map projection you choose, some projections may cause distance between features on a map to be preserved while distortion is introduced to shape. In some cases, the area may be preserved while the direction is distorted.
Cartographers choose map projections that best represent the purpose, size, and shape of the area of interest on the map.





Can you please share the notes
Thanks for the nice lecture. But, I can’t get about the map projections.
Thanks so much for the great content! Small correction: Please note that the maps labeled “North America” should be called “Continental United States”.
Fixed it. Thanks!
Thanks for the lecture
Over the period of time there is a buzz about Galls projection being better to represent the earth as compared to mercators …. I wish to hear your opinions about it . Also can you suggest hat kind of activities can I do with kids or assign them to know the differences better
Hello,
I’m fairly new to GIS as my background is from Software Development.
Does this mean a 3d map is better than a 2d map when developing a GIS application/
Thanks!
Earth is spherical or ellipsoidal having curves or curvature. Then why do we convert the 3d globe into planer co-ordinate system. Where as distance, shape and areas are already preserved on globe (that is itsoriginal shape). Distance measured incorporating the curvature of the earth will be accurate.
We know the Earth is Flat served on a plate. Why carry on the deception?
The SURFACE of the earth is two dimensional – we need only lat/lon to specify a place’s location!
Map projections preserve this 2-D topology.
pride of a geographer,