Georeferencing: How to Georeference Images
When you take any ordinary image and give it real-world coordinates, you are georeferencing it. You can stretch, scale, rotate, and skew the image to better relate to physical space.
If you want to learn how to georeference, then follow these 3 easy steps.
- Add control points.
- Select a transformation or rubber sheeting method.
- Check your RMSE.
Follow this georeferencing tutorial on how to georeference with precision.
Step 1. Add Control Points at Matching Locations
How do you put any image into a geographic context?
The answer is simple:
You’ll need to find something that already has real-world coordinates. In other words, you need anything that is georeferenced already.
You then use it as the reference image for control points. Control points are specific locations commonly found in two images.

Do yourself a favor and find the most suitable image possible. For example, if you want to georeference an aerial photo taken in 1920, you should use a reference image closest to that date for better control points.
Once you find that reference image, it’s then a matter of finding matching targets in both scenes.
- Click on a specific location in the first image you want to georeference.
- Next, click on the reference image matching location.
- Repeat until you have four (preferably more) control points.
In the end, your image will have the coordinate system that’s set in your data frame.
While there’s no perfect number of control points, it completely depends on the scan of your image and RMSE.
Step 2. Select a Transformation
When you are georeferencing, you stretch, scale, rotate and skew the image to better relate it to physical space.
Generally, an affine transformation is sufficient for georeferencing. An affine transformation preserves straight lines in two-dimensional space by scaling, rotating, translating, and skewing the image.
Alternatively, rubbersheeting gives more flexibility by bending and warping images through a third-order polynomial equation. A higher polynomial allows more bending and warping of an image.
Although a third-order polynomial may be useful if there is significant distortion in the scanned image, you will typically use affine transformations for georeferencing.
Step 3. Check Your Root Mean Square Error (RMSE)
A good rule of thumb is that a low Root Mean Square Error (RMSE) means a better-georeferenced image.
However, a low RMSE does not necessarily mean that your image is fitted on the Earth’s surface any better.
As you add more control points, the RMSE measures how well these control points fit that particular affine or polynomial equation.
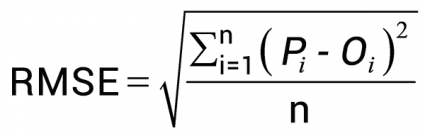
When you change the transformation method, you’ll see that higher polynomials lower your RMSE value. This is because those control points can better fit that equation to mathematically stretch your image into two-dimensional space.
But when you inspect your image, it warps in areas where you have fewer control points. Overall, if your scan is high quality such as mylar, then you should select a simple affine transformation.
How Georeferencing Works
You can take any drawing, any schematic, and put that image into a geographic context. You can even take it a step further and vectorize those features and query them.
Now, it’s time to take the training wheels off. You have all the core knowledge to georeference with precision.
The steps are simple:
- Add control points
- Select a transformation
- Check your accuracy using RMSE
Try it out in ArcGIS Pro with this how-to georeference video.



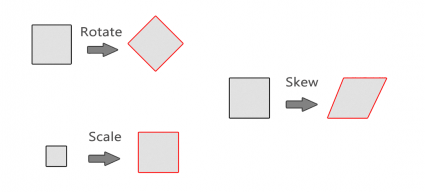
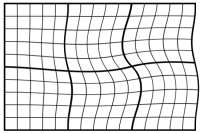








The affine transformation is basically a linear model so it is appropriate for flat landscapes. It would not be appropriate for example, for air photos taken in mountainous terrain. It is fine for maps because they have a constant scale, and air photos from flat landscapes such as floodplains.